J1 = 0 if J* ≤ μo,
Ji= 1 if μ0 < J* ≤ μλ,
J1 = 2 if μ < J1 ≤ μ2,
J1 = 3 if μ2 < J*.
where J1* = x1'α+ ε1 ; x1 is a vector of exogenous characteristics of individual 1; and ε1 is a
disturbance term. The characteristics include gender, marital status, English speaking ability, race
(black, white, and other), ethnicity (Hispanic and other), age, age squared, education, education
squared, US farm experience, US farm experience squared, and the year of interview (before 1993,
after 2001, and in-between).4 We assume that ε1 is normally distributed with a mean of zero and a
standard deviation of σε. Then the likelihood function can be expressed as
where Φ(∙) indicates the cumulative distribution for the standard normal.
L (α, σε, μj | data) =
Ji =0
<
φ∣ μ0- xα ∣ ∏
I σε JJ Ji ='
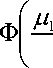

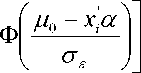
∏
J1=2
..'
μ2 — xiα I ɪ I μ1 - xiα It-T1 ɪ( μ2 - xiα I
—---1- I - Φl —---1- ∏ 1 - Φl —---1- I
σ J I σ J J=3 I σ J
ε ε Ji =3 ε
(1)
Suppose the cumulative distribution function of farm work duration (tij) for person i with
legal status j is given as
Fij(t)=Pr(tij <t).
We denote its density function as fij(t). The probability for the spell to be of length of at least t,
usually called the survival function, is given as
Sij(t)=1-Fij(t).
4 See the Data section below for additional detail.
More intriguing information
1. A Location Game On Disjoint Circles2. Learning and Endogenous Business Cycles in a Standard Growth Model
3. A novel selective 11b-hydroxysteroid dehydrogenase type 1 inhibitor prevents human adipogenesis
4. The name is absent
5. POWER LAW SIGNATURE IN INDONESIAN LEGISLATIVE ELECTION 1999-2004
6. sycnoιogιcaι spaces
7. Managing Human Resources in Higher Education: The Implications of a Diversifying Workforce
8. The name is absent
9. Initial Public Offerings and Venture Capital in Germany
10. The Institutional Determinants of Bilateral Trade Patterns