Non-causality in Bivariate Binary Panel Data

Table 1: Mnemonics for the estimated models

models, together with the degrees of freedom as reported in the following scheme:

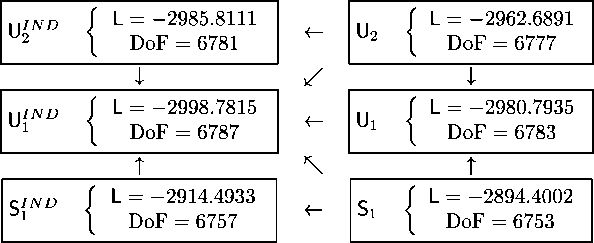
The possible restrictions are indicated by an arrow connecting the two boxes:
in particular, if a box connects model M^t (U for unrestricted') to model M^h (R
for restricted), we say that model M^h is nested in model M^σ. Therefore, we
can test all the restrictions through a Likelihood Ratio test;¹⁵ in particular, if
we indicate by Ljy the log-likelihood of the unrestricted model and by the
log-likelihood of the model obtained after constraining some of the parameters,
the Likelihood Ratio test consists in calculating the statistic

2 ∙ (Lb - L_σ).

This statistic is asymptotically distributed as a where p is the number of pa-
rameters constrained in the restricted model. The results are reported in Table
3 and show that all the restrictions are refused at any conventional significance
level (90%, 95%, 99%). Clearly this procedure is not able to discriminate be-
tween two models that are not directly linked by a restriction, and therefore, we
cannot say whether U₂ fits the data better than Si, since they are non-nested.
Therefore, in order to select a model, we calculate two widely used criteria for
the comparison of non-nested models: the AIC (Akaike Information Criterion)
and the BIC (Bayesian Information Criterion, due to Schwarz, 1978); in both
cases the model maximizing the criterion is selected. The formulas are the

—---------------

¹⁵See Gouriéroux, Monfort and Renault (1987) for a similar testing strategy.

19

<<   16   17   18   19   20   21   22   >>

More intriguing information