rather then a (3JH)-dimensional vector. Consequently, notation may be simplified as
follows for all j -1,..., J :
( j -1) H + h =: h (12)
jH =: H (13)
j β( j-1)H + h,2 j-1 =: βh,2 j-1 (14)
j β(j-1)H+h,2j =: βh,2 j (15)
j Y(j-1)H+h =: Yh (16)
3.3 A Mathematical Description
The network architecture described above implements the general class of neural
models of singly constrained [SL] spatial interaction
ωsl ( x, w ) j = Ψj
2j
π
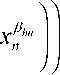
j 1, ..., j
(17)
with φh : H → H, ψj : K → K and a (2 J) -dimensional vector
x (x1, x2, ∙∙∙, x2j-1, x2j, ∙∙∙, x2J-1, x2J )
(18)
where x21 represents a variable sj pertaining to destination j ( j = 1, ∙∙∙, J) and x2j a
variable fj pertaining to the separation from region i to region j ( i = 1, ∙∙∙, I ; j = 1, ∙∙∙, J )
of the spatial interaction system under scrutiny∙ βhn (h = 1, ∙∙∙,H; n = 2j -1,2j) are the
input-to-hidden connection weights and γh (h = 1, ∙∙∙, H) the hidden-to-output weights
in the j-th module of the network model∙ The symbol w is a convenient shorthand
notation of the (3H)-dimensional vector of all the model parameter ψj (j = 1, ∙∙∙, J)
represents a non-linear summation unit and φh (h = 1,∙∙∙,H) a linear hidden product
unit transfer function∙
12
More intriguing information
1. DISCRIMINATORY APPROACH TO AUDITORY STIMULI IN GUINEA FOWL (NUMIDA MELEAGRIS) AFTER HYPERSTRIATAL∕HIPPOCAMP- AL BRAIN DAMAGE2. Beyond Networks? A brief response to ‘Which networks matter in education governance?’
3. The name is absent
4. Learning-by-Exporting? Firm-Level Evidence for UK Manufacturing and Services Sectors
5. Critical Race Theory and Education: Racism and antiracism in educational theory and praxis David Gillborn*
6. Modelling the Effects of Public Support to Small Firms in the UK - Paradise Gained?
7. The name is absent
8. The Challenge of Urban Regeneration in Deprived European Neighbourhoods - a Partnership Approach
9. Evaluation of the Development Potential of Russian Cities
10. Perfect Regular Equilibrium