5th and 8th grade pupils’ and teachers’ perceptions of the relationships between teaching methods, classroom ethos, and positive affective attitudes towards learning mathematics in Japan

234

ethos varies from one classroom to another. In addition, pupils within the same
classroom may have different perceptions of classroom ethos. Overall, 5^th graders were
significantly more likely to perceive satisfaction, friction, and competitiveness in
mathematics classes than 8^th graders. 8^th graders were more likely to perceive difficulties
in mathematics classes than 5^th graders. There was no significant difference in their
perceptions of cohesiveness (see Figure 7.3.1 and Table 7.3.1).

Figure 7.3.1: Mean scores of pupils’ perceptions of classroom ethos in mathematics
classes

5

4

3

2

1

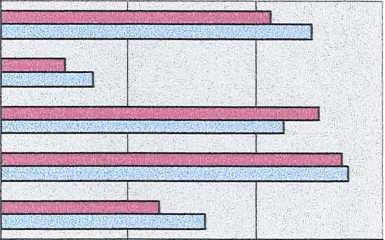
□ 8th graders

□ 5th graders

0  12  3

I=Satisfaction, 2=Cohesiveness, 3=Difficulty, 4=Friction, S=Competitiveness

Table 7.3.1: Mean scores and standard deviation of pupils’ perceptions of classroom
ethos in mathematics classes

Correlations were undertaken between the sub-scales for students of both age groups. A
significant positive correlation existed between satisfaction and cohesiveness, among
the responses of pupils of both age groups, although the correlations were relatively
weak. There was also a weak but significant correlation between friction and
competitiveness among the responses of 5^th graders (Table 7.3.2).

234

<<   245   246   247   248   249   250   251   >>

More intriguing information