particular vessel-vehicle for organising all goods shipments, which we have made up
to now in order to employ the formula ti= vi/ Qi in our logistics model, seems to be
very limited and inappropriate for most real world situations, given that logistics
calculations normally involve fleet management considerations, in which the optimum
size of the vehicle-vessel is the key question. However, we can adopt a similar
approach as in section 4, but now extend it to the case of multiple vehicle-vessel sizes.
Where we have a range of vehicle-vessel types and sizes to choose from, we
consequently also have a range of values of vi which can be included into the
calculation formulated in equations (4) to (7). Each different value of vi will generate
a different Qi* and for the firm the value of Qi* which is the most preferable is that
particular value of Qi* , which over the range of vehicle-vessel choice alternatives,
minimises the minimum total logistics costs calculated on the basis of any particular
vessel type i.e. the optimum optimorum. If there are multiple vehicle-vessel types and
sizes to choose from, each type with its own particular shipment capacity limit, the
usual logistics approach is to calculate the optimum shipment frequency for each
mode of transport, assuming that we are constrained to use a particular mode of
transportation, and then to compare the relative minima of each of these vessel
options. Such an approach is used to determine the general size, frequency, vehicle-
vessel mode and size of individual deliveries, and one of the aims of the logistician
will be to ensure maximum vehicle-vessel capacity utilisation, i.e. full load shipments
of individual vehicle-vessels where at all possible, although as we have seen, full-load
vehicle-vessel utilisation will not be the primary criterion governing the organisation
of shipment deliveries.
We cannot know the value or behaviour of the parameter t in a type (a) model
involving multiple vehicle-vessel choices without a priori knowledge of the values of
all the other parameters. However, it is possible to provide a general principle.
Individual vessel or vehicle types often tend to exhibit shipment economies of
scale. In other words, when we compare the relative costs of movement between
different vessel or vehicle types and sizes, we see that the variation is normally much
less than proportionate to the relative carrying capacities of the vessels (Jansson
1980). In other words, if we plot the per-mile movement costs vi against the full-load
carrying capacity Qi for each vehicle-vessel, over a range of vehicle-vessel sizes and
types, i=1.......n, in general we will see an upward sloping relationship as shown in
Fig.5.
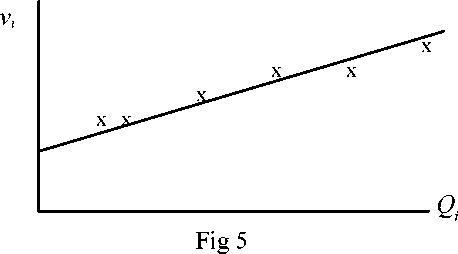
The relationship between vessel movement
costs and vessel carrying capacity
11