Optimal Vehicle Size, Haulage Length, and the Structure of Transport Costs

The paper is organised as follows. In section two, we will outline how these
issues have previously been dealt with in the literature and indicate the analytical
problems that these explanations create. In section 3, we will discuss the relationship
between two different analytical specifications of the shipment size optimisation
problem. The first approach specifies transport rates as a function of the distance and
quantity of the bundle of goods to be shipped, while the second approach specifies
transport rates in terms of vehicle-vessel haulage costs. We will see that at present
these two approaches do not give us consistent analytical results to the problem of the
relationship between the optimum shipment size and the haulage distance. Therefore,
it is necessary to unify the approaches to the specification of transport rates in these
two models in order to produce coherent results. In section 4 this is done initially for
the case of a single vehicle-vessel. In section 5 this unified approach is then extended
to the more general case where we have multiple vehicle-vessel choices. In section 6
we will provide a formal proof of the conditions under which the vehicle-vessel size
increases with the haulage distance. This will also allow us to prove that transport
rates are almost always concave with the haulage distance irrespective of whether or
not we experience economies of scale in vehicle-vessel hauling costs, and irrespective
of the number of vehicle-vessel choices we have. The reason for this is due to the
calculation of the optimum shipment size itself. Finally, we will be able to explain the
conditions under which haulage costs are convex with respect to the haulage weight.

2. The Problem

Within transport economics, there is as yet no formal analytical proof of the
conditions under which the optimum size of a vehicle-vessel increases with haulage
distance. The problem centres around the well-known paradox that observed freight
rates per ton normally taper with haulage distance as in Fig 1., whereas the observed
cost per ton of a given vehicle or vessel is generally linear with distance, as described
by Fig.2.

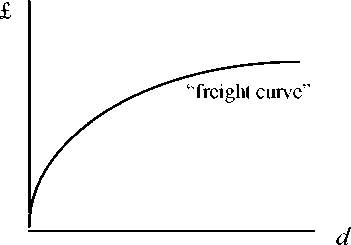
Fig. 1

Freight rate per ton tapering with distance

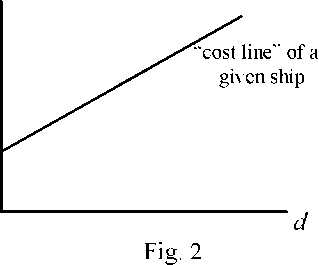
Costs per ton as a linear function of distance

The existing ‘indirect proof’ by Thorburn (1960) in the case of water-borne shipping
has been described by Jansson and Shneerson as “a possible point of departure” (1982
p.226) and “a useful diagrammatic technique” (1987 pp.144-145). The same argument
was also employed by Alonso (1964) in the case of road and rail shipments.
Thorburn’s heuristic approach is explained by Jansson and Shneerson thus:

<<   1   2   3   4   5   6   >>

More intriguing information