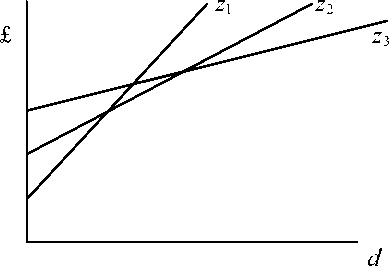
Fig. 3
Costs per ton for different ships as a
function of distance
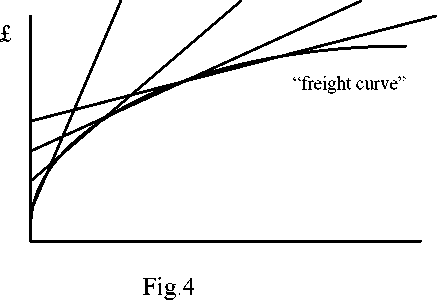
The freight curve as an envelope to
cost lines of given ships
When we compare the cost per ton functions of various alternative vessels of
increasing size,z 1,z2 ....zn, if we assume that the port or terminal handling costs per
ton, represented by the positions of the intercepts, and the vehicle-vessel hauling costs
per ton, represented by the function slopes, behave as described according to Fig.3,
Jansson and Shneerson (1982; 1987 pp144-145), argue that we can draw an envelope
function as described in Fig 4. Observation of the point of tangency between a
particular vehicle-vessel function and the envelope suggests that a larger vehicle-
vessel will be used for longer routes. However, there are two fundamental problems
with this heuristic approach.
(i) The theoretical validity of such an analysis depends crucially on the there being
both a sytematically positive empirical relationship between the size of an individual
vehicle-vessel and its terminal or port handling costs, and a systematically negative
empirical relationship between the size of an individual vehicle-vessel and its hauling
cost per ton. Otherwise, it would not be possible for us to draw Fig.4. Moreover, these
systematic relationships would also need to hold empirically in the case where we
have vehicle-vessels of different vintages, in spite of the fact that technological
improvements which reduce the port or terminal handling costs and movement-
hauling costs will be embodied in newer vehicle-vessels. In the case of marine
shipping, the empirical evidence of Heaver and Studer (1972), Robinson (1978) and
Garrod and Miklius (1985) indicates that no such systematic functional relationships
as described in Fig.3 necessarily exist. Indeed, if Fig.3 was altered to take account of
their findings, the optimum vessel size on all routes would be extremely large, as
Garrod and Miklius (1985) correctly point out.
(ii) It is not possible to use observed cost per ton freight rates with respect to distance
and quantity of the bundle to be shipped, as exogenously determined inputs to the
problem of the optimum vehicle-vessel size. The reason is that such observed freight
rates themselves depend on the fleet management principles employed by third-party
hauliers using their own fleets of vehicle-vessels. The result is that such an approach
cannot tell us how the optimum size of a vehicle-vessel is related to haulage distance.
All it can tell us is how the optimum size of a shipment, belonging to a customer who
does not make decisions concerning the optimal employment of vehicle-vessels, is
More intriguing information
1. HEDONIC PRICES IN THE MALTING BARLEY MARKET2. On the job rotation problem
3. Feeling Good about Giving: The Benefits (and Costs) of Self-Interested Charitable Behavior
4. The name is absent
5. The name is absent
6. Evidence on the Determinants of Foreign Direct Investment: The Case of Three European Regions
7. Ronald Patterson, Violinist; Brooks Smith, Pianist
8. The Impact of Hosting a Major Sport Event on the South African Economy
9. The name is absent
10. Giant intra-abdominal hydatid cysts with multivisceral locations