coordination allows individual countries to raise more revenue, politicians will
therefore want to spend all of the increased revenue on expanding public sector
employment, apart from any revenue that may be needed to continue satisfying
the recruitment constraint. ¥
Proof of Proposition 5: Using (2.11) and (2.15), the social welfare function (2.5)
may be written as
SW = αu (W + rk) + (1 — a) u (w (r + τ) + rk) + g (a) ,
which may be differentiated to give (using w0 = — k and the fact that (1 — α) k = k
in symmetric equilibrium):
dSW
dτ
= 0 initially
da 0 dW -
• dτ + aug ∙ ɪ + ak
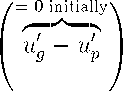
dr
dτ
— kUp. (A.31)
0 Z“}|“{
g0 + ug — up
Inserting (4.3) through (4.5) into (A.31) and remembering that ug = up, u0g = u0p
and dW = dw initially, we find by using w = FL that
dSW
dτ
μ u0k
a + εa-1 (1
_
∖2
a)
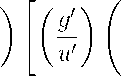
ε (1 — a)2
wa
u0kε (1 — a)2
a2 + ε (1 — a)2
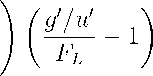
+ a — £a + εa (1 — a) ]
(A.32)
Equation (A.32) shows that the welfare gain from tax coordination is proportional
to the initial degree of underprovision of public goods, f g-/u-
— 1 , as measured
by the deviation from the Samuelson condition which requires g-/u- = 1. From
Proposition 3 we know that equation (3.4) must hold in the initial tax competition
equilibrium. Inserting this expression for g^u- into (A.32), we finally obtain
dSW
dτ
u0kε (1 — a)2
a2 + ε (1 — a)2
(⅛ )(
(1 — a))
—1
> 0.
¥
(A.33)
38
More intriguing information
1. The name is absent2. The name is absent
3. NATIONAL PERSPECTIVE
4. The name is absent
5. XML PUBLISHING SOLUTIONS FOR A COMPANY
6. The resources and strategies that 10-11 year old boys use to construct masculinities in the school setting
7. The name is absent
8. MULTIPLE COMPARISONS WITH THE BEST: BAYESIAN PRECISION MEASURES OF EFFICIENCY RANKINGS
9. Fiscal Sustainability Across Government Tiers
10. Strategic Policy Options to Improve Irrigation Water Allocation Efficiency: Analysis on Egypt and Morocco