S Δ0
(1 —S2) ^BA + b
SS⅛-2za ' SS⅛-2za
1
for
for
b ∈ [0,
S∆B0A ]
’ (1-S2) ]
SΔ3'0
sδba
(1-S2)
and
^70-1(^) = S
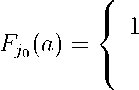
S Δ30-1
(1—S2) δab ∣__a
SSm—(>o+1)ZB + SSm-(J0+1)ZB
for
for
a ∈ [0,
S Δ30
s δab
where
(1-S2
S ∆A0B
(1-S2

b
S Δ0-1
(1 —S2) δab
1
for b ∈ [0, 'AB ]
, , S δA0b 1
for b > T-aBt •
Δ⅛λ = [⅛m-*>Zb - Si°Zλ] and ∆⅛1 = Ao1Z, - δm-l*0~-ZB].
(12)
(13)
(14)
(15)
Note first that this equilibrium candidate has the properties described in
Proposition 1. Players’ continuation values can be stated as functions of the
respective state j as follows:
( & Zλ for j<jα - 1
vλ(j) = ^ (⅛'-` Zλ - r-(70-1)Zb] for j = jo - 1 (16)
I 0 for j ≥ jo
and
( δm- Zb for j>jo
vb(j)={ (⅛) Г-0 Zb - ^ Zλ] for j = jo (17)
I 0 for j ≤ jo - 1∙
These constitute the payoffs stated in the proposition. For 0 < j < jo - 1,
player A wins the next j battles without any effort. This takes j periods and
explains why the value of the final prize must be discounted to 57Zλ. Also,
B does not expend effort in these j battles and finally loses after j battles.
Hence, B’s payoff is equal to zero. For m > j > jo, players A and B simply
switch roles.
Turn now to the states jo - 1 and jo as in Figure 2. We call these states
"tipping states", because of their pivotal role in determining the outcome
of the contest. Consider jo - 1. From there, if A wins, the game moves to
jo - 2 with continuation values vλi∕o - 2) = 570-2Zλ and vb(jo - 2) = 0.
13
More intriguing information
1. Nietzsche, immortality, singularity and eternal recurrence12. The name is absent
3. Modelling Transport in an Interregional General Equilibrium Model with Externalities
4. DETERMINANTS OF FOOD AWAY FROM HOME AMONG AFRICAN-AMERICANS
5. IMMIGRATION AND AGRICULTURAL LABOR POLICIES
6. Spectral calibration of exponential Lévy Models [1]
7. The name is absent
8. Nonparametric cointegration analysis
9. Types of Cost in Inductive Concept Learning
10. The Values and Character Dispositions of 14-16 Year Olds in the Hodge Hill Constituency