Trade Liberalization, Firm Performance and Labour Market Outcomes in the Developing World: What Can We Learn from Micro-LevelData?

ity function, as in Krugman (1980). The production side of the economy is characterized by a

continuum of firms, each producing a different variety. The technology features plant-level scale
economies and is summarized by a total cost function as in equation (1), TC(φ) = f + q∕φ. The
only difference is that now firms have different productivity levels, indexed by φ. Hence, φ cap-
tures firm heterogeneity in this model. Firms face a demand curve with a constant elasticity σ > 1.
Profit maximization implies the familiar mark-up pricing rule, p(φ) = σ~l ± . Firms’ profits are
then π(φ) = r(φ)∕σ — f , where r(φ) is revenue. It can be shown that the ratios of any two firms’
outputs and revenues only depend on the ratio of their productivity levels:

Equation (6) and the expressions for p(φ) and π(^) show that more productive firms (i.e., firms
with a higher φ) are bigger, charge a lower price and earn higher profits than less productive firms.

The equilibrium aggregate price index P is a generalization of the standard price index associ-
ated with a CES utility function:

P=

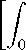
p(φ)^{1 σ} nμ(√)d√

(7)

where μ(^) is the equilibrium distribution of productivity levels and n is the equilibrium number
of firms. Using the expression for p(φ), the price index can be written as:

π      — t— ʌ      — ^{σ 1}

P = n^1-σ p(φ) = n^1-σ----- —

σ — 1 φ

where ⅛5 is the weighted average of firms’ productivity levels. Note that the inverse of the price
index equals real per capita income W (i.e., W = P^-1). Hence, as in Krugman (1980), both
an increase in the number of available varieties n and in the average productivity ⅛5 raise real
per capita income and welfare. However, while in Krugman (1980) the average productivity is

<<   6   7   8   9   10   11   12   >>

More intriguing information