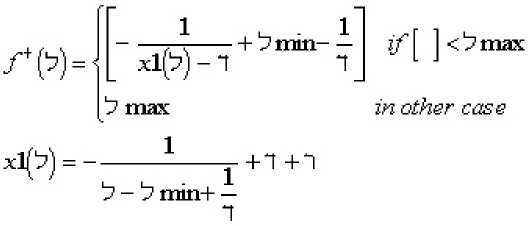
(17)
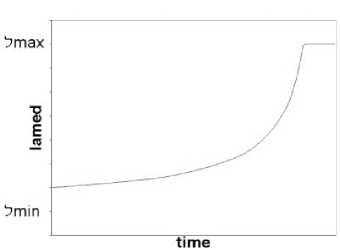
Figure 17. Increase of -.
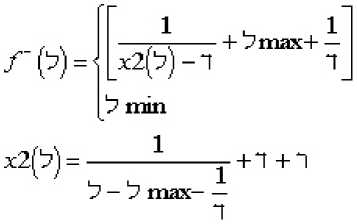
;/[ ]>⅛min
in athsr сas s
(18)
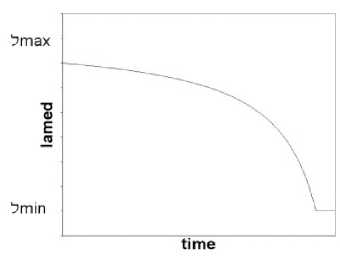
Figure 18. Decrease of -.
where $ (dalet) determines the length of the divergence and 9 (reysh) determines the speed of
the divergence of - bounded between -min and -max. Expression (17) can be seen as a
hyperbolical divergence from -min, as seen in Figure 17, and expression (18) as a hyperbolical
divergence from -max, as shown by Figure 18. The parameter " in BeCA is adjusted using
similar expressions21 (Gershenson and Gonzalez, 2000). Because of the hyperbolical
divergences, once a -k value reaches the neighbourhood of either -max or -min, it will be
difficult that it will leave the neighbourhood. Therefore, for low values of $ and/or high values
of 9, there is a strong dependence on the initial conditions.
The hyperbolical divergences simulate a persistence of the imitation factor over time,
so that it does not jump linearly every time the individual imitates or not a behaviour. This gives
a smoother transition of the values of -k, and it makes -max and -min to be attractors.
21See Section 3.8.2.
58
More intriguing information
1. Workforce or Workfare?2. Consciousness, cognition, and the hierarchy of context: extending the global neuronal workspace model
3. SAEA EDITOR'S REPORT, FEBRUARY 1988
4. Accurate and robust image superresolution by neural processing of local image representations
5. Policy Formulation, Implementation and Feedback in EU Merger Control
6. Has Competition in the Japanese Banking Sector Improved?
7. The name is absent
8. Stable Distributions
9. An Estimated DSGE Model of the Indian Economy.
10. The name is absent