Social Balance Theory

The model and example we presented above is nonetheless realistic only for
small amounts of agents since the reference for change or not-change dyadic relations is
laid upon the global balance index. The algorithm is however advantageous to find the
configuration of balanced group from any initial states.

To have it more realistic, we do some modifications by incorporating the concept
of locality in group. Heider’s principles of social psychology are based on naive
psychology; the psychology as understood by individuals, from which they take any
decisions and some changes of behavior.

To cope with larger group more realistically, we use the concept of local balance
index in addition to the global one. The difference with the previous model is that the
mutation or the change of dyadic sentiment relation is accepted when it can raise the
local balance index. The local balance index is defined as the number of the balance
triads formed by one interpersonal relation (one edge) dividing by all possible triads
formed by the corresponding relation, not by the whole triads in the network as in the
first model.

Tbalanced denotes the number of balanced triads formed by corresponding dyad x-y, Tlocal
denotes the total number of triads formed by the dyad. In the local triads formed by the
dyad we focus on, J is the number of balanced triads and I is the number of all the
corresponding triads.

Global Balance Index

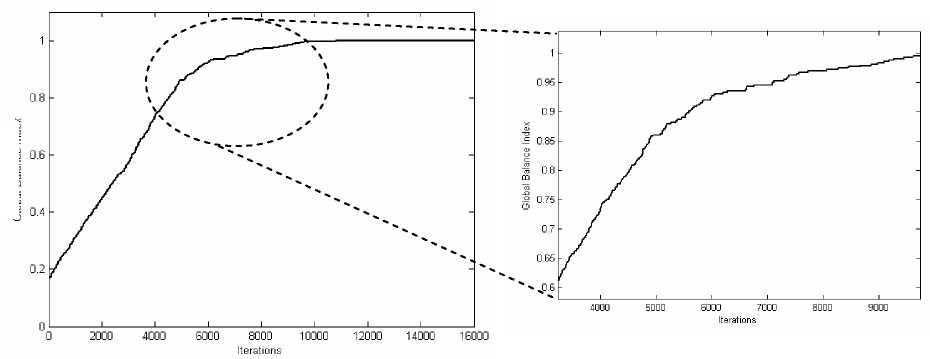
Figure 4

The road to balanced state of N=50 agents after 16000 iterations is almost smooth from initial
global balance index.

For example, the group consists with 50 members (figure 4), the 1225-dyadic
sentiment relations can construct 19600 triads. When the dyadic sentiment relation is

<<   6   7   8   9   10   11   12   >>

More intriguing information