of width, H = 10σ. The segment-segment and the segment-surface interactions were
the same as in the previous case (figure 4.6a). The theoretical results are in good
quantitative agreement with the results from simulation from Cao and Wu [112]. The
density of segment “A” is higher than the density of segment “B” near the surface
and both reach a uniform value away from the surface. Again, uncertainty in the true
state point of the simulations prevents a rigorous test of the theory [125].

Figure 4.7: (a) Comparison of the density profiles of A segments (black) and B segments
(gray) from modified iSAFT and (curves) and molecular simulation (symbols: A segments
(∙) and B segments (■)) for the copolymer BBBBAABBBB in a selective slit pore. The
reduced energies are given by e* a = 5.0, e^,β = —5.0, eAA = 1.0, eBB = 0.5 and e*AB = —0.5
and the average packing fraction of the copolymer in the pore is η = 0.1. The simulation
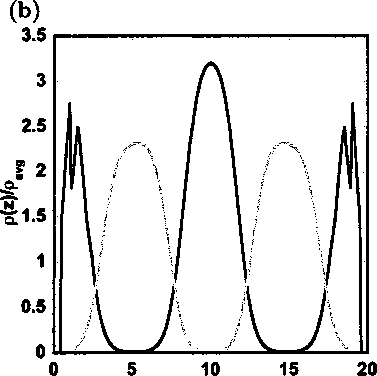
results are from Cao and Wu [112]. (b) Modified iSAFT prediction for the microstructure of
symmetric diblock copolymer of 50 segments (25A25B) in a selective slit pore. The density
profile of A segment is shown in black and B segment in gray. The reduced energies are
given by e^A = 1.0, ejuβ = —1.0, caa = 1.0, c*bb = 0.5 and cab = —0.5 and the average
packing fraction of the copolymer in the pore is 77 = 0.1.
z∕σ
The next system considered is a triblock copolymer “BBBBAABBBB” confined in
a pore of width, H = 10σ. In this case the walls are strongly selective, ewA∣kT = 5 and
106
More intriguing information
1. The name is absent2. DEMAND FOR MEAT AND FISH PRODUCTS IN KOREA
3. Citizenship
4. Rent-Seeking in Noxious Weed Regulations: Evidence from US States
5. Migrating Football Players, Transfer Fees and Migration Controls
6. Weak and strong sustainability indicators, and regional environmental resources
7. The name is absent
8. Mergers and the changing landscape of commercial banking (Part II)
9. The name is absent
10. The name is absent