The name is absent

The Euler-Lagrange equation for a segment β is given by

lnp^(r) +

____ ₁ m {^r'} p

L∈Γ(0) 7=1 7' ^J

P^s*⁹{^

δ∖ny^_tact{{p_β^e9^}∖
δp^s₀^e9(r)

dr I

δβA^ , δβA^^ττ _
δp^f^(r) ⁺ δp^s_β^e∖r) ⁰

(4.47)

Eqn. 4.47 can be further written as

ln⅛'⁹(r) + £ lnX'(r) = ¾(r) +‰, - v_β≈<(r)), (4.48)

A∈Γ(<^j)

where D₀(r) is given by

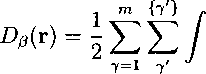
P7(rι)

^lny2X_taci[{⅛^es(r₁)}]

<^s(r)

δβA^εx

,hs

¼^es(r)

δβA^ATT<^s(r)

(4.49)

Physically, lnp^^es(r) + ∑2a∈γ<*³) hiʌ^(r) — hιpθ^eg(r), where Po^e,s(^r) ɪɛ the density of

monomers [58],
since bonding at a site on a segment is assumed independent of bonding at the other
sites on the same segment. For the first segment,

ÆW = ∕>ΓW ∏ ⅛.

A∈Γ(0)

(4.50)

lnp₁(∏) + ln%i^υ(r₁) = A(rι) + β(μι - VΓ(∏)), (4.51)

109