5.2 Model system and theory
The symmetric diblock copolymer molecule is modeled as a freely jointed chain
of tangentially bonded spheres (segments) of two types. One type of segment forms
the ‘A’ block and the other type forms the ‘B’ block. Each block has N segments.
Although both type of segments have the same segment size, σ, they have different
long range attractions. These attractions are modeled as a perturbation to the 6-
12 Lennard-Jones (LJ) potential in the spirit of Weeks-Chandler-Anderson (WCA)
perturbation theory [120, 121].
≤(H = *
uaβ(rmin) uaβ(rc)
uaβ(r) - uaβ(rc)
ff ^aβ < f ≤ ʃ'min
ɪf rmin <r <rc
(5.1)
where rmin = 21∕6σαzj is the position of potential minima, rc = 3.5σaβ is the potential
cut-off distance and
Uaβ(r) = ⅛aβ
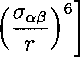
(5.2)
The energy parameters, = евв = ɛ and eAB — O- Hence in the model, e quantifies
the incompatibility between the two blocks of the diblock copolymer. Traditionally,
this incompatibility has been characterized by the Flory-Huggins interaction parame-
ter, χ. As discussed by Frischknecht et. al. [50], for a symmetric diblock copolymer, χ
can be related to the incompatibility parameter e for the continuous potential model
118
More intriguing information
1. Does adult education at upper secondary level influence annual wage earnings?2. Uncertain Productivity Growth and the Choice between FDI and Export
3. The name is absent
4. The name is absent
5. Determinants of Household Health Expenditure: Case of Urban Orissa
6. Natural hazard mitigation in Southern California
7. Konjunkturprognostiker unter Panik: Kommentar
8. The name is absent
9. Surveying the welfare state: challenges, policy development and causes of resilience
10. The name is absent