27
The linearized synaptic input in (2.30) has the form
-⅞ynaptic(^, ʃ; f⅛)
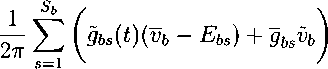
δ{x - Xba).
To complete the linearization process, we equate the terms of order ε and arrive at
c Fc
∂tvb = T>bvb + Kb(x)υb + 52 ΣL dbcj(x)wbcf + Ль
c=l /=1
∂twbcf(t) = φbcf(x)vb + ψbcf(x)wbcf,
where
ɪ l-' ɪ kjb
КьИ = ~^-∑ Gbc(τ)Fbc(0) - ∑9bsδ(x ~ ¾)
m c=l m s=l
1 _ Fc
dbcf(x) = -γr-Gbc(x)(υb - Ec)qcfwqbccff ɪ ɪɪ ¾
___1_
r∣b 2πabC,
sb
∑gbs(t')δ(x - xbs)(υb - Ebs)
s=l
Φbcf(β'')
wc∕,∞(^⅛)
τcf(υb) ,
Mx}=^⅛)'
It is now apparent that this is a linear system for the 6th branch, namely
More intriguing information
1. Conditions for learning: partnerships for engaging secondary pupils with contemporary art.2. Applications of Evolutionary Economic Geography
3. Julkinen T&K-rahoitus ja sen vaikutus yrityksiin - Analyysi metalli- ja elektroniikkateollisuudesta
4. Testing for One-Factor Models versus Stochastic Volatility Models
5. ANTI-COMPETITIVE FINANCIAL CONTRACTING: THE DESIGN OF FINANCIAL CLAIMS.
6. The English Examining Boards: Their route from independence to government outsourcing agencies
7. Three Policies to Improve Productivity Growth in Canada
8. The name is absent
9. Nurses' retention and hospital characteristics in New South Wales, CHERE Discussion Paper No 52
10. Feature type effects in semantic memory: An event related potentials study