The name is absent

ɪ = A_feξ(i) + B_feu(t), y(t) = C_feξ(i),            (2.39)

where

Afc = (WfVfc)^-1WfcAVfe, Bfc = (WfV_fc)-¹WfB, Cfe = CV_fe. (2.40)

The reduced-order system is computed by finding V∕_c and W⅛ so that the L2-n0rm
of the error between the transfer functions of the original and reduced systems along
the imaginary axis is minimized, i.e., we solve the optimization problem

min
V_b W_k

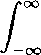
IlC^τ(iωl - A)^-1B - Cf(zωl - A_fc)-¹Bfc∣∣²dω.

One strategy for solving this is to interpolate the full transfer function, to first order,
at the negative of each of its poles. Since these poles are not generally known a
priori and may be hard to compute, we make an initial guess and then iterate until
convergence, indicating that we have arrived at the reduced system. This is achieved
in a computationally efficient manner via the Iterative Rational Krylov Algorithm
(IRKA), whose implementation details are found in (Gugercin et al., 2008).

I give the IRKA algorithm here for the multiple-input multiple-output (MIMO)
case, which is exactly what we have in the quasi-active system.

<<   43   44   45   46   47   48   49   >>

More intriguing information