The name is absent

the case of current injection, v_mi_d is the solution to the linear system

(21 / ∆t — H + diag(Φ(w^)e))v_mid = 2v^ ŋ/ʌi + Φ(w^w)E_i — ɑɑɔ,(v — E_s), (3.8)
where v is the rest potential of the discretized system.

3.2 The Reduced Cable Equation

We apply two model reduction techniques to this ODE system, both of which
use the proper orthogonal decomposition (POD). The first technique generates a
low-dimensional basis for the state variables, v and w, while the second generates a
low-dimensional basis for the nonlinear term.

3.2.1 Proper Orthogonal Decomposition

Given that v ∈ R^7v, we wish to find a subspace Z√ C R^7v of dimension к ≪ N in
which the relevant states v are nearly contained. Specifically, given n “snapshots” of
the state variables X = [ξ(tι) ξ(⅛) ■ ∙ ■ ξ(2_n)], we wish to find an orthonormal basis
{≠i}√=₁ C R^7v that solves the minimization problem

n

min
{<M,L1

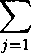
к                   2

ξ⅛) “ ∑(ζ(^tj)^τΦ^Φi ,
2=1                2

i.e., we desire the ^-dimensional basis that best fits, in the least squares sense, the
snapshot data (Kunisch and Volkwein, 2002). The proper orthogonal decomposition

<<   70   71   72   73   74   75   76   >>

More intriguing information