124
Solve the characteristic equation s2 + 2as + ωθ
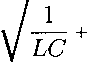
Rj
LCRm
1 R1
O' — -———— -f∙ ---
2CRm 2L
-2a ± ʌ/4cv2 - 4ω2
^ 1
3~~2CRm
ʌʃɪ
2L V v 2CRm
-^1)2 _ /_!_ +
2L} yLC LCRm
Now sɪ and S2 are defined, along with ω0 the resonant frequency (in radians∕sec) and a the
damping factor
We look for a solution of the form υ(t) = K1es1t + K2es2t + K3
We need to solve for K1, K2 and K3 from the final and initial conditions
K1e~o° + K2e °° + K3 = is(R1∖∖Rm)
■ ⅛[K1e∙>< + ¾e∙=< + ¾] = ⅛∣ho = ≈√Cm
Kie0 + K2e0 + K3 = υ(0) = 0
K3 - ⅞ ( .Ri I ∣,Rto ) - is β11+‰
■ s1K1 + s2K2 = ^∖^ = is∣Cm
K1+ K2 = -K3
Now the system is fully defined
More intriguing information
1. The name is absent2. Critical Race Theory and Education: Racism and antiracism in educational theory and praxis David Gillborn*
3. Placenta ingestion by rats enhances y- and n-opioid antinociception, but suppresses A-opioid antinociception
4. The name is absent
5. Education and Development: The Issues and the Evidence
6. Feeling Good about Giving: The Benefits (and Costs) of Self-Interested Charitable Behavior
7. The Response of Ethiopian Grain Markets to Liberalization
8. The name is absent
9. Biologically inspired distributed machine cognition: a new formal approach to hyperparallel computation
10. The name is absent