15
cylindrical symmetry of the system and discretize the p-z plane on a triangular mesh using
a finite element scheme, which reduces the system to 2D effectively.
3.1.2 BdG Formalism
Let us consider a Fermi gas distributed in two hyperfine spin states. The Fermi system
across a broad Feshbach resonance, which is realized in 6Li or 40K atoms, can be well
described by the single-channel Hamiltonian as following:
fH =
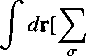
ψl(r)Ho-ψa(r) + g^J(r)^J(r)^(r)^τ(r)],
(3.1)
with the creation and annihilation operators of fermions, ≠τr(r) and ≠σ-(r).
Following the procedure in Reference [22], we can obtain the Bogoliubov-de Gennes
(BdG) equations [21] which take the form
where the single-particle Hamiltonian is given by
H↑ ∆(r)
∆*(r) -H1
ui(r) ui(r)
= Ei
v,(r) v,∙(r)
(3.2)
Hσ = -n2V2∕(2m) + Veχt(r) - μσ(cr =↑, J,) (3.3)
The quasiparticle energies E7 take both positive and negative values. The order parameter
and the densities are given by Δ = g X, uiv*f(Ei), n↑ = X1 ∣u,∣2∕(E,), and ni = Xl∙ ∣v,∣2∕(-E,∙)
where f(E) = [exp(E∕kT) + 1]~1 is the Fermi distribution function and the densities must
be constrained as N↑,i = ʃ dr n↑j(r), g is the bare coupling constant which will be replaced
by the s-wave scattering length as via the regularization prescription: (4πħ2as∕m~)~l = l∕g+
More intriguing information
1. Evidence of coevolution in multi-objective evolutionary algorithms2. Consciousness, cognition, and the hierarchy of context: extending the global neuronal workspace model
3. Keynesian Dynamics and the Wage-Price Spiral:Estimating a Baseline Disequilibrium Approach
4. Developments and Development Directions of Electronic Trade Platforms in US and European Agri-Food Markets: Impact on Sector Organization
5. The name is absent
6. Migration and employment status during the turbulent nineties in Sweden
7. The name is absent
8. Does Presenting Patients’ BMI Increase Documentation of Obesity?
9. Behavioural Characteristics and Financial Distress
10. CONSIDERATIONS CONCERNING THE ROLE OF ACCOUNTING AS INFORMATIONAL SYSTEM AND ASSISTANCE OF DECISION