The name is absent

Rectilinear Drawing          69

√ ∕*^3π                            d f- .

— ⅛ /        ɛɪɪɪ ^{= -}J      ^{sιn w})^^w∙

Thus the equation under consideration is equivalent to
ξʃ Hι(r')dr = ʃ²Λ^w (r sin u)du,

at least if the function Я1(г) is suitably restricted near r =0.
For example, it would suffice if we assumed that H_i(r} re-
mains finite near r=0. But the right-hand member is
evidently the same as

/■ ⅛₁w (ʃ)- ≠-,

J Vrⁱ-Sⁱ

so that the equation is essentially a linear integral equation of
Abel type for hχ'∖s}. Hence we obtain

'^s r{f^r_aHV₁')drι')dr
∙∖Λ² — r²

where the outer integral in the right-hand member clearly
vanishes for r=0 and has a continuous first derivative.
Hence this equation is equivalent to

, ; ч _ i d^i
hl^~2π dsⁱ

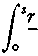
(J^r_aHV₁)df₁')dr~ _
V sⁱ-rⁱ   -

Thus we infer that a necessary and sufficient condition for
a solution to exist is that the integral on the right side of the
equation just written admits a continuous second derivative,
in which case the unique solution is provided by the same
equation.

But the double integral on the right may clearly be
written in inverse order of integration as

о ∖J∣Vj²-f²/ Jo

<<   20   21   22   23   24   25   26   >>

More intriguing information