government. The government now maximizes the welfare function:

πdA +
∕∙n+
AAh
dB
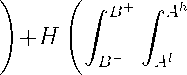
и (F -
∙.K) dAdB^
(22)
with π and v* defined as in (14) and (15), subject to
F(K,Al) (1 - и) - (1 - au) K = О
(23)
F(K,Aft) (1 - и) - (1 - au) K = F (K*,Aft) (1 - t) - (1 - βt) K* - C(24)
The optimality condition with respect to и is:
∂W ['b+ Ah ['b+ A"
-— = Q = Ud' - U')J J [(F - aK)] dAdB + H'J J [u (Fκ - a) Ku] dAdB
+h ' C (u (f ft -aK η 9~a-) dB
h ' £ (u (fl
., ∂Al∖
aKl) — dB (25)
7 du J
The optimality condition with respect to a is:
∂W
da
Zb+ Ah B++ Ah
I [uK] dAdB + H' I [u (Fκ - a) Ka] dAdB
+( h' ι (F‘- aK' > ■)dB - £ h' (u fl - aKl) ) b'
First, it follows from equation (25) that u > О, a = 1, H' = U' cannot be an
optimum, because
dw =£ h' (u (f (AK'■) - k^) d-A) dB = 0 (27)
Second, u has to be greater than zero to satisfy Д^" = 0. This can be explained
as follows: The first term on the RHS of equation (25) is strictly positive, the
three other terms are strictly negative. Therefore, u = 0 and u < 0 are no possible
solutions.
Can u > 0, a = 1, H' > U' be an optimum?
12
More intriguing information
1. Quelles politiques de développement durable au Mali et à Madagascar ?2. Globalization, Redistribution, and the Composition of Public Education Expenditures
3. Evaluation of the Development Potential of Russian Cities
4. Monetary Discretion, Pricing Complementarity and Dynamic Multiple Equilibria
5. Developmental Robots - A New Paradigm
6. The name is absent
7. FOREIGN AGRICULTURAL SERVICE PROGRAMS AND FOREIGN RELATIONS
8. The Role of Evidence in Establishing Trust in Repositories
9. Personal Income Tax Elasticity in Turkey: 1975-2005
10. Orientation discrimination in WS 2