Figure 1
Non-stochastic Steady State
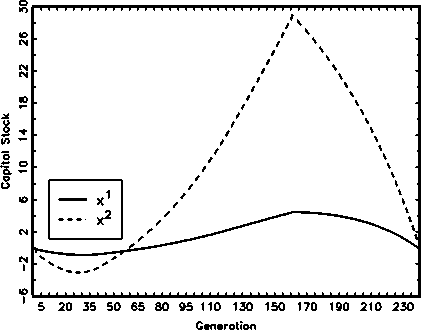
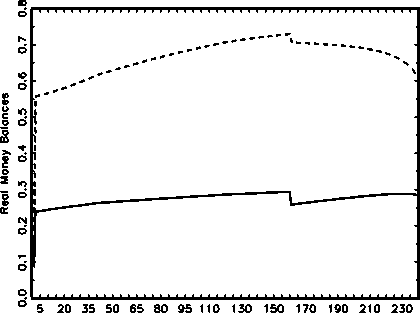
Generotion
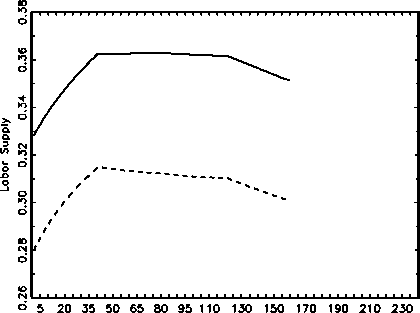
Generotion
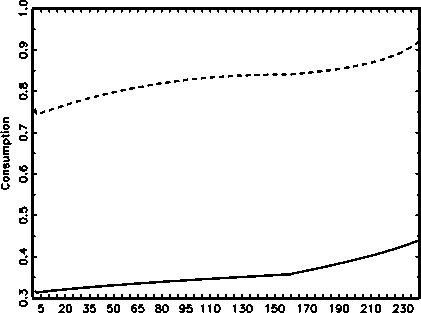
Generotion
wealth in our model is also close to the one observed empirically. In our model, the
Gini coefficient of wealth amounts to 0.64, whereas Greenwood (1983), Wolff (1987),
Kessler and Wolff (1992), and Dlaz-Gimenez, Quadrini, and Rlos-Rull (1997) estimate
Gini coefficients of the wealth distribution for the US economy in the range of 0.72
(single, without dependents, female household head) to 0.81 (nonworking household
head).13 Our model only fails to model the wealth concentration among the very rich
agents. In order to replicate the wealth distribution of the top quintile, one had to
introduce entrepreneurship as in Quadrini (2000).
calculate the Gini coefficient using only six observations to approximate the Lorenz curve.
13Huggett (1996) shows that we are able to replicate the empircally observable heterogeneity of
wealth in a computable general equilibrium model if we introduce both life-cycle savings and individual
earnings heterogeneity.
16
More intriguing information
1. Group cooperation, inclusion and disaffected pupils: some responses to informal learning in the music classroom2. The Role of Evidence in Establishing Trust in Repositories
3. The name is absent
4. Migration and Technological Change in Rural Households: Complements or Substitutes?
5. Naïve Bayes vs. Decision Trees vs. Neural Networks in the Classification of Training Web Pages
6. THE CHANGING RELATIONSHIP BETWEEN FEDERAL, STATE AND LOCAL GOVERNMENTS
7. The name is absent
8. WP 1 - The first part-time economy in the world. Does it work?
9. The name is absent
10. he Virtual Playground: an Educational Virtual Reality Environment for Evaluating Interactivity and Conceptual Learning