The name is absent

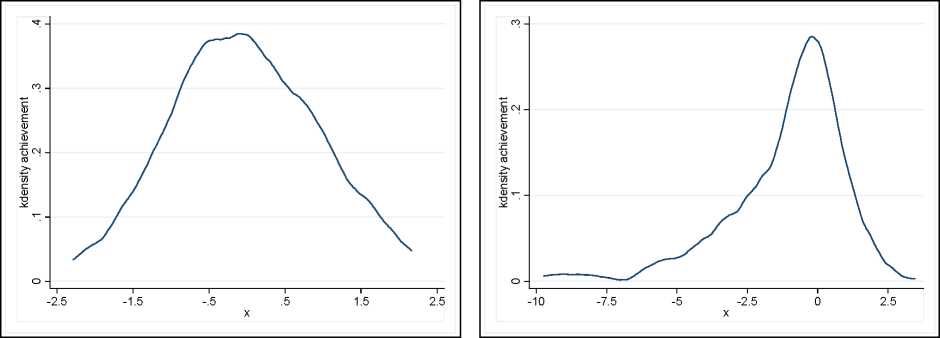
presented in Figure 1b has a long left tail, illustrating that some countries, mostly developing
countries that participate less frequently in international tests, have low student achievement.

Figure 1. Kernel density of student achievement

a) “Core” country observations               b) All observations

In a fixed effect model, identification is only based on within-country variation. Figure 2
shows the development over time for the “core” countries. The figure indicates that there are
some systematic changes. For example, the relative achievement in the more neo-liberal
Western economies USA, Canada and UK increased during the 1990s, while the achievement
declined in Israel and in the transition countries Russia and Hungary. Some countries perform
consistently better than others. For example, Italy performs below average and Netherlands
performs above average in each test. However, Figure 3 shows that there is quite some
variation in the change in student achievement, although the variation is lower than that for
the distribution in levels of achievement.¹⁰

4. Model specification

We estimate the following model for student achievement Z of country i in year t

Zit = βιgit +β2 log(GDP / POP)it +β3 log(POP)it +β4EDUit +Φi +Φt +εit               (7)

where git is a measure of the welfare state, discussed in detail below, while GDP per capita
(GDP/POP) is the proxy for y in (6). Family characteristics as parental income and education
have strong effects in micro studies of student achievement, which is why we also include the

⁹ Hanushek and Wossmann (2007) use as their “core” countries 13 OECD countries with “stable education
systems”, but they do not report which countries.

¹⁰ In Figure 3, only observations with at most eight years interval are utilized.

<<   8   9   10   11   12   13   14   >>

More intriguing information