17
MDx ■ Xe {>} Ye
xee
if
X >0 and/or X >0 and X =0,
ra1ra2rc
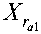
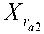
=Xr=0,
rc
(23)
X =X =0 and X >0.
ra1 ra2 rc
To derive (22) from (21), we first consider (21f) and (21g) to obtain — = —----
λfλf
λ
= 1 + — X, . Next we combine this equation with (21a) to turn (21b) into
λf c
λx
λf
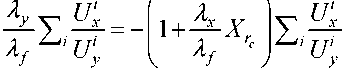
Uxi
∑iuiy
(24)
Ui
1+X ∑Ux
rc iUi
f U U1 ^ r
In (24), 1 + Xrc ∑Uχ ∈]0,1[
к Uy J
y
since λx∣λf > 0 in an interior solution. We proceed by infer-
this equation into (24).
λx
ring x
λf
Ye
Xe +Σ jXrajRe
from (21c), (21h) and (21k). (22) is then obtained by inserting
Clearly, (22) characterizes the efficient level of pollution generated jointly via the emission of
all residuals. MDx is the damage from a marginal increase in pollution evaluated by the con-
sumers' aggregate marginal willingness-to-pay in terms of the consumer good for avoiding
that increase. The right side of (22) represents the marginal benefit of pollution that comes in
form of an increase in the consumer good made possible by a small increase in pollution
through stepping up emissions. Equivalently, one can interpret MDx as the marginal benefit
and YeQ∕Xe as the marginal cost of reducingpollution. To further interpret the term YeQ∕Xe
observe that Ye is the amount of consumer goods that cannot be produced anymore when the
emission of production residuals is reduced by a small amount. It is known as marginal
abatement costs of production residuals (in terms of the consumer good) in models where no
residuals other than production residuals are considered. For convenience, we will refer to Ye
as conventional marginal abatement costs of production residuals.
If we multiply both sides of (22) by Xe we obtain MDx ■ Xe = Ye ■ Q. The left side of this
equation represents the marginal benefit of reducing the emission of production residuals and
More intriguing information
1. Partner Selection Criteria in Strategic Alliances When to Ally with Weak Partners2. The Determinants of Individual Trade Policy Preferences: International Survey Evidence
3. Fiscal Rules, Fiscal Institutions, and Fiscal Performance
4. Qualifying Recital: Lisa Carol Hardaway, flute
5. The Impact of Individual Investment Behavior for Retirement Welfare: Evidence from the United States and Germany
6. Existentialism: a Philosophy of Hope or Despair?
7. Willingness-to-Pay for Energy Conservation and Free-Ridership on Subsidization – Evidence from Germany
8. Centre for Longitudinal Studies
9. REVITALIZING FAMILY FARM AGRICULTURE
10. The name is absent