Nonlinear Production, Abatement, Pollution and Materials Balance Reconsidered

20

(i) Suppose, that λ₁ ,λ₂ ,λ_c,λf,λ_t, λ_m, λ_x and λ_y are the values attained by the Lagrange
multipliers in the solution to (20) and that the partial derivatives X_e and R_h^j for j = 1, 2 and
h = £,m are also evaluated at that solution. Set prices p_t = λ_f>,p_m = λ_m,p_y = λ_y and con-
sider the alternative tax schemes A and B:

-Aisdefinedby:  tA = λ1, t _; = λ₁, tcA = λ_c, tA = λxXe and tA = t^AA = 0 ;

^-B^isde^finedby:  ^tB = ^tB2 = 0^{, t}CB = ^λc^{, t}eB = ^λxXe ⁺∑ _j ^λjRe ^, t£ = Σ _j ^λ-R  and

tm^B =∑_jλjRm^j .

With these prices and either tax scheme A or tax scheme B all markets clear and the equilib-
rium allocation is efficient.

(ii) When the tax scheme A is implemented, the efficient tax rates satisfy

X_r > 0 and/or X_r > 0 and X_r = 0,
ra1ra2rc

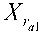
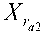
=Xr=0,
r_c

X=X=0 and X>0.

ra1         ra2                      rc

To prove Proposition 4i insert the prices and tax rates as assigned in Proposition 4 into (27)
and verify that this substitution makes (27) coincide with (21). The tax scheme A in Proposi-
tion 4i is a pure emissions tax scheme in the sense that a tax is levied on the emission of each
polluting residual, while non-emission items like the inputs labor and material are not taxed.
We infer from (21) that (in equilibrium) with the tax scheme A all tax rates are set equal to the
marginal environmental damage of the respective residuals¹⁵:

t^A = MD X : = -∑ ^x . ^v for v = e,r_a,r_a ,c
vxv    i i        a₁a₂

U_y

We also know that if abatement takes place, optimal emissions tax rates need to equal mar-
ginal abatement costs. In our model production residuals are the only residuals subject to
abatement. Therefore we will now focus on those residuals. Invoking (27b) we obtain, after
some rearrangement of terms,

te^A=Ye-∑ ta^AjRe^j-tc^AYe.                                                             (30)

ee  aece

¹⁵ To simplify the comparison of marginal conditions characterizing either efficient allocations or market alloca-
tions we measure all prices and tax rates in terms of the consumer good by setting p_y ≡ 1 .

<<   19   20   21   22   23   24   25   >>

More intriguing information