The name is absent

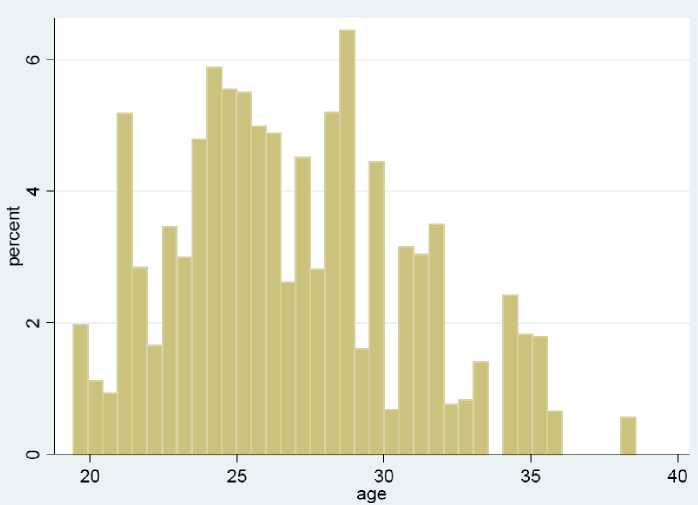
Figure 5: Distribution of age (on May 17, 2008) of players from nations that qualified for the
Euro 2008. The sample excludes goalkeepers, and Austrian or Swiss players. The number of
players is 165.

this information is more readily available, and the starting age for a professional career
in soccer, as in most other sports, does not seem to differ much across players. Figure 5
shows the distribution of age for players in the treatment group.

The basic regression equation we wvill use to test for differential effects as a function
of age is

Yint = at + Yi + δoqualified_nt + διqualified_nt (age_i - age_i)
+ μ₁after_t (μge_i -age-) + X'_mtβ + ε_mt,

where an upper bar denotes the mean over players in the treatment group. To capture the
possible non-monotonicity predicted lay the nomination contest theory, we also estimated
regressions including interactions terms with the (demeaned) square function of age_i and
other more complex Sunctions, or dummies fod different age groups based on percentiles
of ths age distribution. None of these analyses yielded significant results, however, which
is wIiy we will focus on the results obtained using a simple linear interaction term as
in (10). The coefficient δ₀ estimates the treatment effect for a treated player oS average
age, while δι tests tor differential effects by age. Since the regression equations already
seem relevant for determining htw well, say, Italy’s national coach knows an Ctalian player.

26

<<   29   30   31   32   33   34   35   >>

More intriguing information