What Drives the Productive Efficiency of a Firm?: The Importance of Industry, Location, R&D, and Size

Mean Efficiency

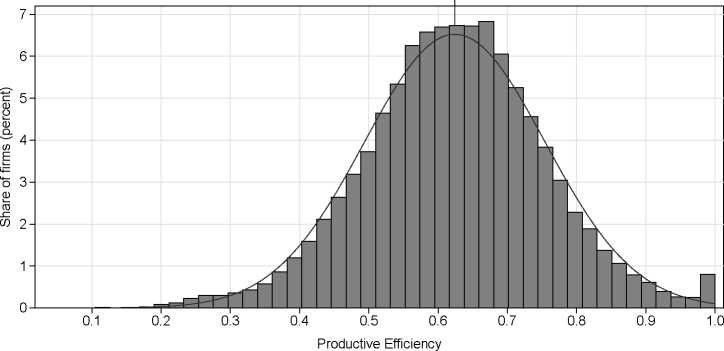
Figure 1: Histogram of efficiency at the micro level and normal density (38,641 observations)

3.4 Distribution of productive efficiency

Table 3 shows the parameters of the distribution of productive efficiency scores calculated ac-
cording to Equation (2). In general, the distribution of productive efficiency is centered and most
firms are clustered close to the mean (Figure 1). The peak seen in distribution at the maximum
level is because, by definition, at least one firm in each industry is fully efficient; that is, each
industry has a different max αjs used as the benchmark in Equation (2) for the other firms in
that industry. Symmetry as well as skewness of the distribution of productive efficiency largely
coincides with the normal distribution. This is reassuring as it confirms the appropriateness of
using OLS in the second step of the analysis.

4 Determinants of productive efficiency

4.1  Partial R²s and variables used in the second step of analysis

To analyze the determinants of productive efficiency, we relate the estimated productive effi-
ciencies to a number of explanatory variables. We employ analysis of covariance (ANCOVA),
where independent variables can be both metric and categorical, as the regression method. Since

Table 3: Distribution of productive efficiency

Variable N    Mean   CV p90    Q3   Median   Q1    p10    min

Efficiency   38641   0.625   0209   0.785   0.707    0.624    0.542   0.461   0.041

Notes: p10 and p90 are the 10^th and 90^th percentiles; CV is the coefficient of variation; Q1 and Q3 are lower
and upper quantiles.

10

<<   10   11   12   13   14   15   16   >>

More intriguing information