where 7 comes from (2) and 'f = (7f,.., 7 J) where 7f is the sth element of vector — (Ir(s)SfIr(s))~1 Ir(s)s(pf)∙
Remark that out of equilibrium retail prices can be obtained from observed equilibrium retail
prices, retail margins at equilibrium and out of equilibrium retail margins using : pfr(s) = 7fr(s) —
(ps — ws — cs)+ ps where 7fr(s) = pfr(s) — ws — cs is the out of equilibrium retail margin∙ Moreover,
pʃ can be deduced from the differentiation of the retailer’s first order conditions with respect to
wholesale prices∙ These first order conditions are, for all r = 1,.., R and VJ ∈ Sr,
Sj (pfr )+ ∑ ' — ^s — Cs) ' .' =0
sCSr ∖Gfr Spj
which gives for r = 1,.., R, J ∈ Sr and s = 1,.., J1
^ ∂sj (pfrjfS) ∂pfrj
S-~f Sffrjjl ∂ws
IC[1,..,J }∖Gfr °pl s
1 ∂ss (7fr(j)) + v Ssi(p-fr(j)) ⅜fω
[sGSr} dpfr(j ^S dpfr(j) ∂ws
1J l^ sr j j
+ Σ
lCSr∖Gfr
(pfr — wι — cι) ∑
sG[1,..,J }\Gfr
a2sl(p'fr(j)) ap'fr(j)
∂pfjrω∂pfsrj dws
(16)
Defining Spf the matrix (J x J) of the second derivatives of the market shares with respect to
retail prices whose element (s, I) is
) ∙ p
affr(f)affr(f) , ∙ ∙
/
Sp ≡
J2f
∖
a2s1 (pfr<f>)
apfr(f)apfr(f)
∙
∙
∙
∂2s1 (pfrt-f~>)
∂pfrωdpfjrf
∂2sj (pfrt-^) ∖
apf,r<f>apfr<f>
∂2sj (ffr<f>)
∂pfr-f∂pjr-f /
we can write equation (16) in matrix form to obtain
FW [sf + irSfp' + (spfIr7fr∣...∣sp;Ir7fr)] Ir — IrSp (ιr — Ir) = 0
where 7fr = pfr — w — c∙
Denoting Mfr the matrix ^S~ + IrSf' + (SpfIr7fr∣...∣SpfjIr7fr)] we can solve this system of
equations and get the following expression for J2W
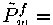
_
f∑r-1 Ir Mf r Ir Sf (Ir
i)) (∑Π1
Ir Mf r Mfr Ir
Equation (15) shows that one can express the manufacturer’s price-cost margins vector as depen-
ding on the demand function and the structure of the industry by replacing the expression for
Ff
^ W ∙
17
More intriguing information
1. The purpose of this paper is to report on the 2008 inaugural Equal Opportunities Conference held at the University of East Anglia, Norwich2. Discourse Patterns in First Language Use at Hcme and Second Language Learning at School: an Ethnographic Approach
3. Investment in Next Generation Networks and the Role of Regulation: A Real Option Approach
4. The Effects of Attendance on Academic Performance: Panel Data Evidence for Introductory Microeconomics
5. The name is absent
6. Placentophagia in Nonpregnant Nulliparous Mice: A Genetic Investigation1
7. Wounds and reinscriptions: schools, sexualities and performative subjects
8. On Social and Market Sanctions in Deterring non Compliance in Pollution Standards
9. The name is absent
10. The name is absent