PER UNIT COSTS TO OWN AND OPERATE FARM MACHINERY

where the bracketed term [•] is the same as that specified in model 1. Both of the scale
parameters (β₃₉ and β₄₀) are expected to be positive numbers. This would result in a positive
scale factor that decreases at a decreasing rate, i.e., ^ β₃₉ + β₄₀

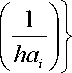
asymptotically approaches

β39 as harvested acres (ha) approaches infinity (Gujarati).

Model 4 uses a logarithmic scale factor to evaluate farm size impacts on the machinery
costs for a farm and is specified as

(5)     tcmc_r=[i]{β₃₉+β₄₀ln(ha_r)}+e_r,
where the bracketed term [•] is the same as specified in model 1. The scale coefficients (β₃₉ and

β₄₀ ) are expected to be positive and negative, respectively. This would result in a reduced scale
factor for larger farms, or increasing returns to scale at a diminishing rate.

A non-linear least squares (NLS) method was used to estimate the models, but resulted in
numerous illogical estimated coefficients (i.e., negative field operation coefficients). Therefore,
an entropy estimation procedure was incorporated in this research to bring in prior information
(published custom rates) about the estimated coefficients, as well as to ensure reasonable
estimates. Using the entropy framework, a prior, or expected value, and upper and lower bounds
are needed for each estimated coefficient and error term. For all operations listed in Kansas
Agricultural Statistics (KAS) Kansas Custom Rates publication for 2001 (Kansas Agricultural
Statistics Service), the prior, upper and lower bounds used were the statewide average,
maximum, and minimum reported values, respectively. For operations not reported in the KAS
Kansas Custom Rates for 2001, priors and bounds for related operations were assigned, or

<<   5   6   7   8   9   10   11   >>

More intriguing information