)LUP %HKDYLRXU
3URGXFWLRQ
Firms operate in a monopolistically competitive environment. Private sector GDP <W is
produced via a nested CES and Cobb Douglas production function with capital .W, energy
(W and private sector employment 1W as inputs. The variable 7.W represents an efficiency
index for the fixed capital stock and the variable 71W represents labour augmenting
technical progress. The following equation describes potential output <327W of the
corporate sector under the assumption that all factors of production are fully utilised.
-г i-Pρ "√1-α) Z α
<327, =(J⅛ -ρ +(1 - D )(, -ρ ] TJ ( 1lT,,)
(4)
Labour augmenting technical progress grows with an exogenous rate π and the efficiency
index for capital, 7.W , captures embodiment effects resulting from current and past
investment. More specifically, it is a function of the mean age of capital $*(W
τ
T = τ 0 $*(
(5)
with
∞ , . Z \
$*( =∣Σ,'+1)(1 - δ) -, J /
defined as the sum of current and non-depreciated past investment as a ratio to the current
stock of fixed capital. Firms may not always operate at full or optimal capacity, therefore
actual output can differ from potential output and we define
< = 8&tYP0Tt
(6)
where 8&W is the rate of capacity utilisation. Capital stock changes according to the rate of
fixed capital formation -W and the rate of geometric depreciation δ
К = Jr - δκr
(7)
Furthermore, it is assumed that the investment process is subject to rising marginal costs of
installation. Total real investment expenditures are equal to investment purchases -W plus
the costs of installation. The unit installation costs are assumed to be a linear function of the
investment to capital ratio. It follows that total investment expenditure ,W can be written as
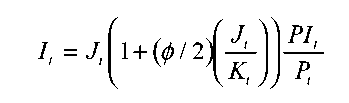
(
(
PL
3
∖
(8)
The objective of the firm is to maximize the present value of its cash flow 09W subject to
a capital accumulation constraint and costs of adjustment associated with capital and labour.
This model of the firm is a slight generalization of Hayashi’s (1982) extension of the
neoclassical model of investment. The maximization problem has the following form
More intriguing information
1. Reconsidering the value of pupil attitudes to studying post-16: a caution for Paul Croll2. The name is absent
3. Evaluating the Impact of Health Programmes
4. Transgression et Contestation Dans Ie conte diderotien. Pierre Hartmann Strasbourg
5. The name is absent
6. An Intertemporal Benchmark Model for Turkey’s Current Account
7. The Global Dimension to Fiscal Sustainability
8. The name is absent
9. Demographic Features, Beliefs And Socio-Psychological Impact Of Acne Vulgaris Among Its Sufferers In Two Towns In Nigeria
10. The name is absent