∞V
0ax09W = ∫[(1 - WF )( P (⅞ ) ) ( KV, 1V, (V )-:V1V - PEs (1 + Wh ) (V - 9&V9$&V )-PIVIV ]expf- W udj 1 GV
(9)
i.e the firm maximises the present discounted value of its cash flow defined as revenue
minus labour, energy and vacancy costs at the rate 9& for each vacancy. Unlike in the case
of perfect competition, it is assumed that firms do not take prices as given but they set
prices by varying the markup according to demand conditions. The solution of the
maximisation problem gives the following behavioural equations for investment,
employment and energy.
,QYHVWPHQW
The optimisation problem yields the following investment rule
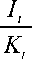
1 f T
φ l( PI, / P, )
Ï
-11
√
(10)
where TW is the shadow price of capital and PIWPW denotes the relative price of investment
goods relative to the GDP deflator. The variable T can be interpreted as reflecting the
present discounted value of the marginal revenue from current investment. This can also be
written as a function of current and discounted future expected profitability, where
profitability is expressed as the ratio between gross operating surplus *26W and the capital
stock. Profitability is adjusted for monopoly rents.
* *2 *GOS,
(1 - WF)(1 - η)-^
k
A×( DT ∖f T ʌ
+φ 33 _L
21p. λ к )
^ S
exp -∫(г
∖ r
. ʌ
+δ)GM1GV
)
(11)
As can be seen from this expression the shadow price of capital is a complex expression and
depends in particular on current and future real interest rates, profitability and effective
corporate tax rates but also on the markup level charged by the firm. The exchange rate can
also affect investment directly by changing the relative price between new investment goods
which are partly imported and domestic output. By explicitly introducing elements of
imperfect competition into the model we can in principle differentiate between the effects
of profitability on investment as derived from improved cost conditions versus higher
markups. The former will generally stimulate investment whereas the latter will generally
lower investment activities. This investment rule assumes that firms do not face financing
constraints.
As can be inferred from equation (10) and (11) the investment equation is entirely
determined by the parameters of the production function, the markup factor η and the
adjustment cost parameter φ. Because of the existence of liquidity constraints at least for
some firms an empirical aggregate investment equation is likely to be more heavily
determined by current profits. A formulation where after tax profits receive a larger weight
compared to discounted expected future profits is given by the following equation.