Lumpy Investment, Sectoral Propagation, and Business Cycles

kj,t = kj,t(1 — δj)∕g and k⁰ = kt. Succeeding mean capital kt^u is defined by the profile
k_j^u_,t. Then k_j^u_,t, u = 0, 1, . . ., evolves according to the (S,s) rule:

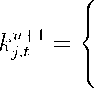
^λj^kj^u,t

^kut∕^λj

k^u
kj,t

if j < ^k

if ^kut > ^λj kt
otherwise

We can show that this dynamics converges at a finite stopping time T with probability
one when N → ∞. Thus the best response dynamics is a valid equilibrium selection
algorithm. Then we define the converged point as an equilibrium capital profile at
t + 1, namely, kj,t+1 = k_j^T_,t.

The best response dynamics is a realistic equilibrium selection mechanism in a sit-
uation where many agents interact each other, as Vives (1990) argues. All information
needed for an agent to make decision is the prices and the mean capital level. This
selection mechanism precludes big jumps that occur due to the informational coordi-
nation among agents. In this sense, the best response dynamics selects an equilibrium
path that is least volatile among possible equilibrium paths.

The aggregate investment fluctuates along the equilibrium path depending on the
evolution of configuration of the capital profile in the inaction region. To evaluate the
magnitude of fluctuations analytically, we regard the capital configuration as being a
random variable that takes values within the inaction region. Specifically, we assume
that the position of an individual capital relative to the lower bound of its inaction
region (in log-scale) follows a uniform distribution independent across sectors.¹ The
uniformity assumption has an analytical ground. It is known that a variable which
grows linearly and is controlled by an (S,s) policy converges to a uniform distribution in
the (S,s) band when the initial value is random. See Engel (1992) for the mathematical
reference and also Nirei (2003) for a rigorous treatment in our specific economic model.

Define a producer’s position in an inaction region as s_j∙,_t = (log k_j∙,_t — log kj,t)/ log λ_j∙.
We assume for a while that λj and δj are common across j. Define m₀ = N (log k¹ -
log k_t)/log λ where k¹ is the mean capital at the first step of the best response dynamics.
At the first step, all capital is depreciated by (1 — δ)∕g and some producers increased
capital due to the direct effect of the depreciation. Thus m0 indicates the deviation of
mean capital growth from the time average level in the unit of the number of producers
at the first step of the adjustment process. Also define W = N (log k_t+1 — log k_t)/log λ.
W indicates the deviation of mean capital growth from the time average level in the
unit of the number of producers in the entire best response dynamics. Define μ =
∣ log((1 — δ)∕g) ∣/log λ. Here we place our main analytical proposition.

¹ See Nirei (2003) for the case in which the distribution is not uniform.

<<   6   7   8   9   10   11   12   >>

More intriguing information