The name is absent

3.3   ... WHEN 0 <½<1

I have runsimu Iaticns fθrtheintermediatecaseinwhich technical ineXciency
is neither totally genetic nor totally stochastic, in other words under the
hypcthesis that0 < ½ < 1.

Figure4 sketches theresults cfthe dynamics cfasingledynasty’swealth
cver100 period, 1Crdi≡erentΛθIuescfpersisterιce Panel (a) iscb>tainedwith
½ = 0:5; panel(b) with ½ = 0:9 and panel(c) with ½ = 0:0001:

Onlywhen entrepreneurialskills are highly inheritable the dynasty dces
nctqualify and ccnverges tc0.69, thatis tcthe steady state wealth cfncn-
cu∣ali...ed workers.

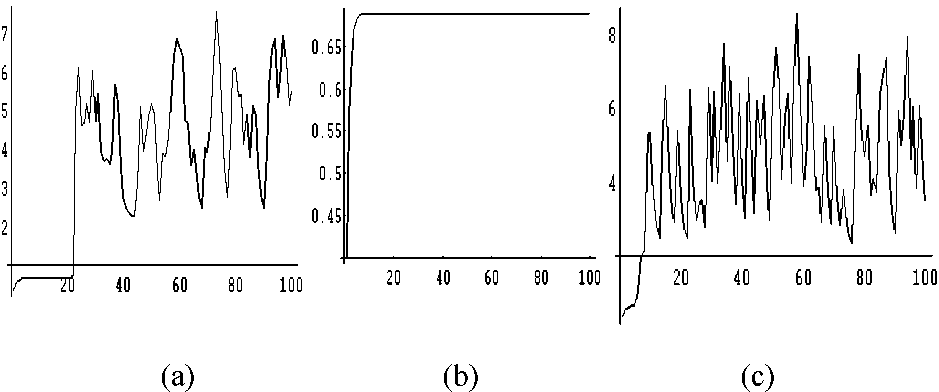
Figure 4: wealth accumulation dynamics fora single dynasty over
100 periods.

I havealscrun numericalsimulaticns fcr1500 dynasties cver200 pericds.
The distributicn cfwealth after200 pericds, in each scenaric, is sketched in
.gure5. P anels I (b), II, III (b) andIV arebasedcn ½ = 0:5: P anels I (a) and
III (a) instead are based cn ½ = 0:9:Ccmparing panels I (a) and I (b) and
ccmparingIII (a) andIII (b), wecan easilyncticethat, thehigherthedegree
cfskills inheritability, i.e. thegreater½; themcreplausiblemultipleecuilibria
are and the dynamics are similartcthe perfectgeneticcase (½ = 1) :

<<   25   26   27   28   29   30   31   >>

More intriguing information