J.Q. Smith and Antonio Santos
fined through the second order Taylor approximation of log f (yt∣αt) around μt,k,
log g (yt αt∙μt,k) x l (μt,k) + l0 (μt,k) (α- μt,k) +1 l00 (μt,k) (α- μt,k¢2 (24)
= const - αt - 2 yt (---γ ( (αt - μt,k) + (αt 2μt,k) - 1! (25)
2 2β exp μttyk) , 2 y
Using this second order approximation, the density g (αt, k|Dt) is factorized as
in equation (15) and the factors are
g (at∖at-I,k,yt,μt,k} = n μt,k,σlk} (26)
and
where
and
g yyt∖μt,k)
exp (2 ɑ + 2β 2 exp ( μt,k )
Л * 2
l μt,k -
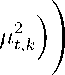
× exp
-_ yt (1 + μt,k)
∖ 2β2 exp (μt,k)
1j+ + yt ʌ 1 ï yt (1 + μt,k ) + μt,k _ 1
σηση 2β2 exp (μt,k)J y 2β2 exp (μt,k) ^1 2
2 β 2 σ П
2β2 + exp (-μt,k) σ2У2
(27)
(28)
(29)
(30)
As we sample from g (αt, k|Dt), an approximating sample, the elements in it
must be resampled in order to obtain a sample that gives a better approximation of
the target density f (αt, k|Dt). The weights used in this resampling step are
log wj
πj
У2
2β2 exp (αt,j )
yt (i_ αt,j (1 _ αj+μt,k ) + ( μt,k+μ2k ´´
2β2 exp μttjβ)
wj
p m=ι wi,
j = 1, . . . ,m
These are the so-called second stage weights that allow the modification of the
approximating distribution towards the target distribution. Obviously, these weights
G.E.M.F - F.E.U.C.
11
More intriguing information
1. The name is absent2. Response speeds of direct and securitized real estate to shocks in the fundamentals
3. The name is absent
4. The name is absent
5. Can we design a market for competitive health insurance? CHERE Discussion Paper No 53
6. Types of Tax Concessions for Promoting Investment in Free Economic and Trade Areas
7. The Structure Performance Hypothesis and The Efficient Structure Performance Hypothesis-Revisited: The Case of Agribusiness Commodity and Food Products Truck Carriers in the South
8. The name is absent
9. Consumption Behaviour in Zambia: The Link to Poverty Alleviation?
10. Optimal Vehicle Size, Haulage Length, and the Structure of Transport Costs