Imperfect competition and congestion in the City

6.4 Long run equilibria

For a fixed level of road capacity s, the free entry equilibrium with congestion
denoted by n^f (s) solves π^e =0. In order to study the free entry equilibrium, we
need to specify the fixed levy per firm S. As the default value, we use S = K .
This leads to a cubic equation, and its solution is not too illuminating. The
profit π^e (s) is a decreasing function of the number of subcenters n. Given
that the equilibrium profit with congestion is larger than without, the free en-
try equilibrium with congestion involves more firms than without congestion:
n^f (s) >n^f.

We can find a lower bound (n^o (s) <n^f (s)) and an upper bound for the
solution of (38). As lower bound, we use n^o (s) that is the solution of the
following equation:

(μd + μ^w )  N + ^δ μɪX — (F + K) = 0.        (39)

n^o (s)    s n^o (s)

We will show in the next section that n^o (s) is the optimal number of firms for
given road capacity and in the absence of congestion charging. Observe that
π^e (n^o) > 0, n^o (s) <n^f (s). So that equation 39 has a unique positive root:

n^o

n (s) = n + —

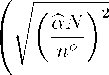
4δ

s (F + S)

where no = (μ^d + μ^w)N/ (F + S), represents the optimum number of subcenters
without congestion (see equation (22)) provided that the firm pays the road
infrastructure cost (S = K).

As upper bound for n^f (s) , we use n^o (s)+1.Wehave:

_{e o           d w} N δ   αbN    ²

^{π (n (s) + 1)}= (^{μ + μ} ) no_η-)⁺ s (∖no (s) + J ^- (F ⁺ K ) .

Subtracting (39) from this equation, we get:

(no + 1) = ^δ (αN)2 I ----¹---- -

s          (n^o +1)²   (n^o)²

As a consequence, n^f (s) <n^o (s)+1.

Summarizing, for given road capacity, in the absence of road pricing and for
an infrastructure charge on firms S = K, we have an upper and lower bound for
the equilibrium number of subcenters where n^o (s) denotes the optimal number
of subcenters.

18

<<   16   17   18   19   20   21   22   >>

More intriguing information