We can be concerned with the distance vector between province i and the province with the
maximum standardised score for an individual indicator (the province with the ideal score).
The length of the distance vector, di containing m components, from the ideal province(s) for
province i is then measured by:
where Zoj is the highest standardised score for indicator j. The lower the di the better the
position of province i relative to the ideal province. We can rank different provinces according
to the value of di. It should be noted that as in the case of the HDI the components of this
regional composite index are treated as having equal weights.
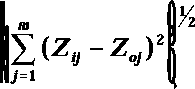
, for i=1,2,...,n
(1)
To continue with the tradition of HDI we may wish to express these measures in the form of an
index whose values remain between 1 and 0. As we have now effectively a single index, though
composite, the re-scaling of the results, to between 0 and 1, will have no bearing on the ranking
order. In fact we have a number of options. We can divide the results by the maximum value in
the set or we may use an approach similar to the one adopted by the UNDP for re-scaling the
results. Alternatively we may follow the approach suggested by Noorbakhsh (1998) and define
our regional modified human development index (RHDI) as follows.
RHDIi = 1 - =d— ,for I=1,2,.. .,n (2)
i d + ksd , ,
where d and sd are the mean and standard deviations of di. The parameter k is determined
such that the value of the second expression on the right hand side of equation (2) for all
provinces would remain between 1 and 0 (as we desire that the value of the RHDI to be
between 1 and 0). Interestingly the selected value for k which would satisfy the above
requirement would also point at the extent of deviation of the distribution from that of the
normal distribution. If the distribution is normal setting k=2 should result in 95% of our
provinces ending up with an RHDI value falling between 1 and 0. For this value of k only one
province (Sistan and Baloochestan) out of 26 fell outside the desired range. In practice for k=2.6
all countries fell within the required range. The results are presented in Table 1. The nearer the
RHDI to 1 the more developed is the province, in terms of the selected indicators, and vice
versa.
More intriguing information
1. Cultural Neuroeconomics of Intertemporal Choice2. The name is absent
3. The name is absent
4. The name is absent
5. New Evidence on the Puzzles. Results from Agnostic Identification on Monetary Policy and Exchange Rates.
6. The name is absent
7. The effect of classroom diversity on tolerance and participation in England, Sweden and Germany
8. Disentangling the Sources of Pro-social Behavior in the Workplace: A Field Experiment
9. The name is absent
10. Subduing High Inflation in Romania. How to Better Monetary and Exchange Rate Mechanisms?