Tables and Figures
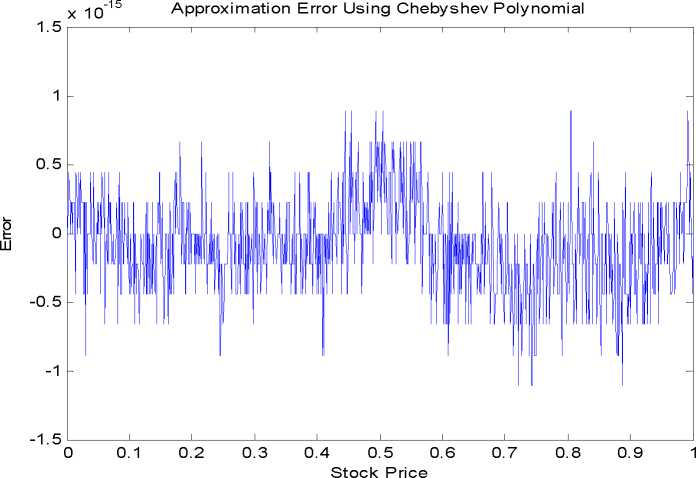
Figure 1
Approximation error using (8) and Chebyshev polynomial when volatility is equal to 0.2
and the interest rate is 0.048.
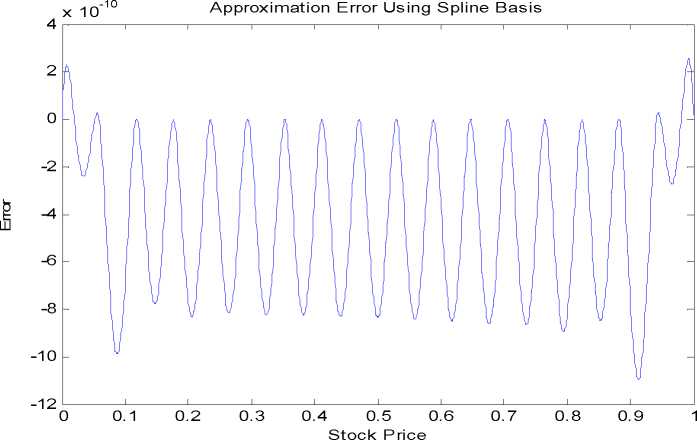
Figure 2
Approximation error using (8) and splines basis when volatility is equal to 0.2
and the interest rate is 0.048
15
More intriguing information
1. A Multimodal Framework for Computer Mediated Learning: The Reshaping of Curriculum Knowledge and Learning2. The Structure Performance Hypothesis and The Efficient Structure Performance Hypothesis-Revisited: The Case of Agribusiness Commodity and Food Products Truck Carriers in the South
3. The name is absent
4. The name is absent
5. DIVERSITY OF RURAL PLACES - TEXAS
6. Why Managers Hold Shares of Their Firms: An Empirical Analysis
7. The Variable-Rate Decision for Multiple Inputs with Multiple Management Zones
8. Federal Tax-Transfer Policy and Intergovernmental Pre-Commitment
9. The name is absent
10. The name is absent