Pj
mi =----j-----M
(3)
j σ
^ V 1-σ 1σ-1
Σ P
L i J
Equation (3) is the compensated demand function for the jth variety.
The minimum cost of attaining a fixed amount of M, can be expressed by using equation (3)
and summing over all the varieties as:
1
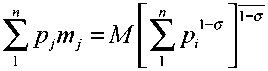
(4)
where the second part of the expression on the right-hand side can be easily interpreted as the
manufactured goods price index:
P = ∑ p^σ
1
1-σ
(5)
P measures the minimum cost of purchasing a unit of the composite index M, and can be
thought of as an expenditure function.
Demand for each variety j can be written as:
mj
Pj
P
-σ
(6)
11
More intriguing information
1. The name is absent2. The name is absent
3. The name is absent
4. The resources and strategies that 10-11 year old boys use to construct masculinities in the school setting
5. Better policy analysis with better data. Constructing a Social Accounting Matrix from the European System of National Accounts.
6. The name is absent
7. DISCUSSION: ASSESSING STRUCTURAL CHANGE IN THE DEMAND FOR FOOD COMMODITIES
8. Sectoral Energy- and Labour-Productivity Convergence
9. The mental map of Dutch entrepreneurs. Changes in the subjective rating of locations in the Netherlands, 1983-1993-2003
10. Review of “The Hesitant Hand: Taming Self-Interest in the History of Economic Ideas”