4. Interest Rates Prediction: Methodology
The expectations hypothesis establishes a relationship between long term (n) and short term (m)
interest rates. The theory asserts that the long term yield can be expressed as an average of expected
future spot rates as implied by Equation (1). We can also say that forward rates are unbiased
predictor of future spot rates.
n-m
[—. A
in
t
-∣∑ Ej-+ mq + tpn
n J q=0
(2)
where itn and itm are the long term and short term yields with maturity n and m respectively (m < n).
The ratio ( -∕n ) should be an integer. The operator Et represents rational expectations conditional to
the information available at time t. The pure version of the expectations hypothesis implies a null
term premium (tptn,m = 0); while the traditional version of EH assumes that tptn,m is simply constant
over time. If the expectations hypothesis holds, i.e. the n-period yield equals the average of the
market’s expectations for the m-period rates, therefore the expected holding period returns are equal
on bonds of all maturities. Developing the summation and ignoring the constant premium we get:
n-m
in
t
I it
nJ
mm
+ 1 - IY Ei-
t t+mq
∖ n J q=1
(3)
Let itn+--- denote the forward (implicit) rate from time t+- to n (the life of the associated artificial
bond thus lasts n-- periods):
i
n
t
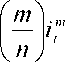
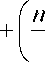
--
n--
Et it+-
(4)
Both sides of (4) must be equal in absence of arbitrage opportunities. Equation (4) simply states that
a -aturity strategy (LHS) must generate the same rate of return of a roll-over strategy (RHS). The
spread, which is a measure of the term structure slope, is obtained on the LHS by subtracting the
short yield from both sides.
The following regressing equation captures the predictive ability of the spread to anticipate future
variations in the short yields movements over the life of the long term bond:
More intriguing information
1. The name is absent2. Restructuring of industrial economies in countries in transition: Experience of Ukraine
3. The name is absent
4. The name is absent
5. THE UNCERTAIN FUTURE OF THE MEXICAN MARKET FOR U.S. COTTON: IMPACT OF THE ELIMINATION OF TEXTILE AND CLOTHING QUOTAS
6. Stakeholder Activism, Managerial Entrenchment, and the Congruence of Interests between Shareholders and Stakeholders
7. What Contribution Can Residential Field Courses Make to the Education of 11-14 Year-olds?
8. Trade Liberalization, Firm Performance and Labour Market Outcomes in the Developing World: What Can We Learn from Micro-LevelData?
9. The name is absent
10. Modelling Transport in an Interregional General Equilibrium Model with Externalities