n-m
∑Eim
t
q=0
t+mq
n-
m
∑Eim
t t+mq
q=0
m nm
- it = α+ β(it - it )+ εt
m nm
-it = α+ β(it -it )+εt
th ≤ ^
th > ^
(10)
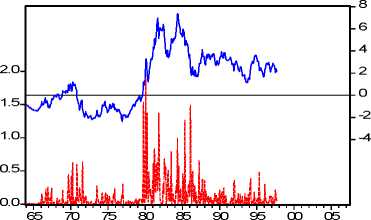
The choice of the term premium as threshold variable (th = tptn,m) allows us to cluster volatility as
well, since the variability of term premia is strictly associated to the level (as shown in Figure 6).
The threshold methodology provides us with a useful framework to separate periods with low
uncertainty from periods characterized by high uncertainty. We recall that the term premium
captures the agents’ sentiment towards risk and is also a proxy for (excess) bonds returns17.
Unfortunately the term premium is not known in advance and is not observable; therefore it is
necessary to make a reasonable forecast18, i.e. to obtain the threshold estimate. Once the estimated
threshold is obtained, economic agents are better informed about which regime will occur in the
future after observing the evolution of the threshold variable. Ideally, after obtaining the threshold
estimate, agents are able to distinguish with certainty regimes on the basis of the observable
dynamics followed by the selected threshold variable. Threshold modelling is appealing because it
acts as an uncertainty reducer. Figure 6 plots term premia and the respective volatility19 for the pairs
of maturities (60, 3) and (120, 3). Volatility seems to be closely related to the level of term premia.
..≈a*v
4.
2-
O.
1-
— tp (60,3) — d^2Jtp (60,3)
1"8
.6
-4
.2
--O
.-2
.-4
τ+⅛l
65 70 75 80 85 90 95 00 05
— tp (120,3) — d^2-tp (120,3)
Figure 6
17 Term premia are perfectly correlated with (log) excess bond returns as computed by Cochrane and Piazzesi (AER,
2005). Term premia reflect market participants’ incapability of anticipating the future evolution of interest rates.
18 Few methods are available to achieve the same objective: Markov switching models, structural change multiple-break
models, and threshold models. The choice of threshold modelling is motivated by the fact that we do not think it is
appropriate to constrain different regimes to be continuous time periods. The threshold framework provides with more
flexibility in characterizing agent’s behaviour with respect to the other aforementioned models. As explained above,
threshold modelling in this paper is employed to distinguish the high uncertainty regime from the low uncertainty
regime.
19 Volatility is computed as the squares of the first differences.
18
More intriguing information
1. Strategic Effects and Incentives in Multi-issue Bargaining Games2. Qualification-Mismatch and Long-Term Unemployment in a Growth-Matching Model
3. TOMOGRAPHIC IMAGE RECONSTRUCTION OF FAN-BEAM PROJECTIONS WITH EQUIDISTANT DETECTORS USING PARTIALLY CONNECTED NEURAL NETWORKS
4. National urban policy responses in the European Union: Towards a European urban policy?
5. Valuing Access to our Public Lands: A Unique Public Good Pricing Experiment
6. The Veblen-Gerschenkron Effect of FDI in Mezzogiorno and East Germany
7. Urban Green Space Policies: Performance and Success Conditions in European Cities
8. The name is absent
9. The name is absent
10. Behavioural Characteristics and Financial Distress