6.3 Proof of Proposition 2
We know that for constant aggregate RRA
Var
Vτ Vτ
ln —
к Vt
Dt
D D D-
= Var I ln —
к Dt
t<τ.
By Proposition 1, for declining aggregate RRA ηtΦ,D, the elasticity ηtS,D > 1
so that the conditional variance of asset returns is higher than the (condi-
tional) variance of the dividend process, i.e.
Var
(l,∙ V
Dt
Dτ
> Var I ln —
Dt
t<τ.
(11)
Consider now the unconditional variance (i.e. θ =0):
Var
(I- S)
Var(E(lnVτ |Dt) -lnVt)+E(Var(lnVτ |Dt))(12)
with
E(lnVτ |Dt)-lnVt
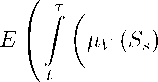
- 1∑V (Ss)2)
ds
We need to show that Var
is greater than
Var
(∣-3
Var(lnDτ |Dt) .
(14)
From (11) it follows that the second term on the right hand side of equa-
tion (12) exceeds Var ɑn D-^. As the first term on the right hand side of
equation (12) is also positive, we are done. The proof is the same for the
variance conditional on Dθ ; 0 < θ < t.
6.4 Proof of Proposition 3
Since by definition CERt- ≡ f- (dSs/ Ss) + f- ( Ds/ Ss — rf ) ds, and the
riskless rate rf is assumed constant, the covariance is given by
Cov ( CERt-,μv (S- ) — rf ∣ Dt) = Cov
---
ddSs DDs D
J Ss- + J S-ds, J dμv(Ss)

22
More intriguing information
1. Testing the Information Matrix Equality with Robust Estimators2. The name is absent
3. Antidote Stocking at Hospitals in North Palestine
4. Education and Development: The Issues and the Evidence
5. Recognizability of Individual Creative Style Within and Across Domains: Preliminary Studies
6. The value-added of primary schools: what is it really measuring?
7. The name is absent
8. Financial Market Volatility and Primary Placements
9. The name is absent
10. Should informal sector be subsidised?