Return Predictability and Stock Market Crashes in a Simple Rational Expectations Model

=E

№+/

Ds,
ST.^ds

dSs     Ds

h+ ⁺ J Ss-^ds

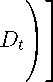
τ

I dμv ( Ss ) - E
t

τ

У dμv (S_s)
t

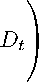
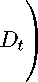
By equation (5), μ_v(St) = ηt^,DηS^,DσD + rf and ΣS(St) = ηS^,DσD. Since
Vt = αtSt , we obtain η_t^S,D = η_t^V,D and ΣV (St) = ΣS(St) = η_t^V,DσD . Hence
we can rewrite the covariance as

τ

f J ηV^,DσDdWs
t

VD ^dηs^,D , Φ,D ^dηV^,D 1 3 DdW
^ηs   ∂Ds^{+ η}s   ∂Ds σDD D^{s   s}

j E ( ʃ v^γrD∂ ^dηs^,D ₊ „ФD ^dηV^,D 1 _σ4 D _ry,D
J ɪs  ∂Ds ^{+ η}s  ∂Ds j^DDD^sηs

Dt ds,

since by Ito’s Lemma the stochastic part of dμ_v(St) is given by

Dt

Φ,D V,D 2

^d ( ^ηt  ^η, ^σD ⁺ r^f ) σD D_t dW_t.

∂Dt

Theelasticities ηV^,D and ηs^,d are positive. Hence, Cov (CERt,_τ,μ_v (Vτ) — rf ∣ Dt) <
[>] 0 if aggregate RRA is declining [increasing] and ηs^V,D is non-increasing
[non-declining] in D_s . The latter condition is equivalent to the condition that
the instantaneous volatility of the return index, ΣV (Ss), is not increasing
[not declining] because ΣV(S_s) = ηV^,DσD.                               ■

6.5 Proof of Lemma 2

Let X denote the aggregate supply of claims. Then equation (9) yields for
ηi(xi)=γi,i = 1...n

1    = ^αi ⁽ X )

ηM ( X )         γi ’

Differentiating with respect to X yields

^ηM⁽ X ) = ^ ^αi⁽ X )

[пм(X)]2 = V Yi '

23