Heterogeneity of Investors and Asset Pricing in a Risk-Value World

Risk

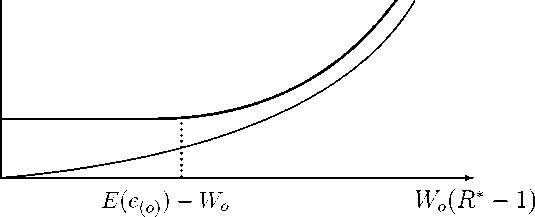
Fig.l The risk-value efficient frontier depicts the minimal portfolio risk as a func-
tion of the required expected portfolio return R*. The thin curve represents
the frontier for an endogenous benchmark, the thick curve for an exogenous
benchmark.

3.2 Risk-Value Models With an Exogenous Benchmark

Now consider risk functions with an exogenous benchmark e; e ≥0. Then in

the first order condition (8) for a risk-value efficient portfolio the second term

disappears since portfolio choice has no effect on the benchmark. Hence the
first order condition reads:

-f (⅛) = ηπ, + A; Vε.

Again, A > 0 so that η < 0 follows.

Taking expectations yields

-E [f (e)] = η + A                        (l3)

so that subtraction of (l2) from (l3) leads to

-E[f (e)] + f (e_ε) = ηθ_ε; V ε.                     (l4)

l5

<<   12   13   14   15   16   17   18   >>

More intriguing information