Heterogeneity of Investors and Asset Pricing in a Risk-Value World

* - (a + ɪ)∕(λ + ɪ)

for 7 > -∞,

l∕B_{i    f}

‰ = 9i = _v^_{1 /p} ^for 7 = ^-∞,
^{l/ l/B}i

3

so that T⅛. = l. Moreover,
i

of the sharing constants, as

define V(ε), a hyperbolic "variance” measure

V (ε) ≡ ×>

i

Ifl ⁽61s^{)/ -} hl ^{- g}l + ^si ^{] 1}

Σ 9jε[^fl ⁽êle^{)/ -} hl ^{- s}l ^{+ s}3)^¹
∖ i

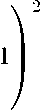
(20)

This variance measure is endogenous since all terms are determined by
the equilibrium. It basically measures the differences between the sharing
constants which are determined by the differences in risk sensitivities and
required portfolio returns (Proposition 5). If all sharing constants are the
same, then this "variance” is zero. Thus, this "variance” tends to increase
with differences among investors in risk sensitivities and required portfolio
returns.

Proposition 9 ; Assume that every investor uses a risk function belonging
to the HARA-class with 7 being the same for every investor. Then for 7 >
-∞ the convexity of the pricing kernel is

C⁽£⁾

- 2

—t [l + V (ε)]
— l

7 — 2 l ⅜ л d^ €{

7 - l ' T (ε) ɪ-'' ^г dε^{2 ,}

∀ε. (21)

30