Conflict and Uncertainty: A Dynamic Approach

^γt ^{- β}iEt^γl₊ι ^{(1 - δ} (st+1))

^αt+ι = (1 ^{- δ}i (st) )^αt + ^zt^xt

We assume ad hoc the following rule for adjusting the subjective valuation:

vi+ι =   ■

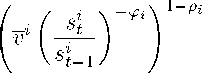
where ρ_t ∈ [0,1] is a smoothin g parameter, φ_t ≥ 0 represents the sensitivity of the rule to the results
from the recent past and

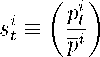
is our “success index”⁸, being vⁱ > 0 the long-run value for the value scale parameter and p^t the
optimal share of the good appropriated by agent i ∈ I in the deterministic steady state.

We are assuming that greater success reduces the value scale parameter for the next period. Note
that in the deterministic steady state we have st = 1 ^and ^vt = ^vt₊₁ = v^t-

The first one of the optimality conditions implicitly defines a “reaction function” of the form

^et = e^t ɑ) '' ,∑^, Rt}

Because the utility function is concave, the cost function is convex and the conflict technology
is concave, then we know that the “reaction functions” are maximizers. By solving the system of
“reaction functions” we obtain the effort levels of equilibrium.

For the case in which all the agents are totally equal to each other, formally ∀i ∈ I, σ_t = σ,

⁸This success index si simply is the difference between what each player really won and what should have won in a
hypothetical steady state.

14

<<   14   15   16   17   18   19   20   >>

More intriguing information