When a positive shock to investment technology of agent one arrives, the share obtained by agent
two is higher with this adaption to harder environment than in the other cases considered. This is
because agent two can adapt to the new technological challenge.
5.3.3 Impulse response with valuation rule
Finally we analyze the impulse response of the conflict model when the scale factor of the valuations
evolves according to the ad-hoc rule
i Qi
vi+ι = (vif M-τ-
∖ ∖δt-1
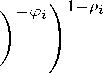
in which the successful agent decreases her valuation for the conflict resource. We are able to replicate
oscillating behaviour on the endogenous variables, specially consumption and investment, but under
this specification it seems harder to get a non-smooth dynamic behaviour of the dissipation.
For example, if we set φ1 = 10 and φ2 = 5 we obtain oscillating consumption:
From the graphics the differences between the optimal paths under different configurations of
the model are clear. The valuation rule induces a longer deviation of effort levels and dissipation
than the other configurations of the model. This implies a higher long-run cost of conflict, because
consumption is away from the long-run path for more time.
5.4 The equilibrium concept
Because of the recursive nature of the problem faced by each agent we can show that there is
dynamic consistency: decisions about future choices made in period t ∈T remain optimal for period
t + j ∈T, j ≥ 0. In a game theory context, this is equivalent as saying that the equilibrium found is
a subgame perfect Nash equilibrium. In this equilibrium we are characterizing the long run optimal
strategies of all the players. Note that the optimal effort level of each agent, and therefore the
reaction functions, are chosen in the same way that they would be in a static game. The dynamics
are incorporated in the determination of the technological parameters, and this is one aspect that
other dynamic conflict models have left behind.
Our model is a truly dynamic one, not only a repeated game model.
19
More intriguing information
1. The name is absent2. Citizenship
3. The name is absent
4. Dementia Care Mapping and Patient-Centred Care in Australian residential homes: An economic evaluation of the CARE Study, CHERE Working Paper 2008/4
5. The name is absent
6. Sector Switching: An Unexplored Dimension of Firm Dynamics in Developing Countries
7. TECHNOLOGY AND REGIONAL DEVELOPMENT: THE CASE OF PATENTS AND FIRM LOCATION IN THE SPANISH MEDICAL INSTRUMENTS INDUSTRY.
8. The Folklore of Sorting Algorithms
9. The Role of Land Retirement Programs for Management of Water Resources
10. Ruptures in the probability scale. Calculation of ruptures’ values