are then contrasted with actual level of beef cow
enterprises for farms of similar size.
Estimation of a Production Possibilities Frontier
The production possibilities frontier for this
analysis was derived with linear programming
methods suggested by Mundlak [131. First, a
standard linear programming problem is maxi-
mized for one objective such as profits; then a
problem is maximized for a second objective with
the problem constrained by the first objective. For
the problem of this paper, the second linear pro-
gram would be of the form expressed in Equation
(4):
(4) Maximize Xi
subject to
Ax ≤ b
c’x ≥ λτro
X ≥ 0
where ττo is maximum profits (under standard
programming methods) and λ is a scalar such
that 0 ≤ λ ≤ 1.
Through parametric programming, the maximum
level of the second objective is determined for
different values of the first. The procedure is then
repeated to determine maximum values of the first
objective subject to varying levels of the second.
These two procedures provide an estimate of the
production possibilities frontier expressed in the
two objectives.
To determine a frontier for profits and beef
cows, this study utilized a linear programming
model of a representative farm developed by Cho-
Chung-Hing [3]. Activities in the model reflected
current production possibilities in the Georgia
Piedmont with good management as recently bud-
geted by Wise [23]. The farm had 243 acres of
open land with 189 acres of cropland and one
full-time farm manager-laborer. The beef cow-
profit frontier from this model is presented in
Figure 1. Points defining this frontier are beef
cow levels and profits at basic changes in the para-
metric linear programming model. Dual values
associated with increasing beef cows are the rates
of transformation between cows and profit. The
rate of transformation is constant between points
presented in Table 2.
Points of particular interest are labelled in
Figure 1. Between points A and B, which have O
and 16 cows, respectively, cows and profits are
complementary. Maximum profits of $10,041 are
achieved with 16 cows. Between points B and E
more cows are possible only with a decrease in
profits. Resources available to the representative
Figure !.PRODUCTION FRONTIER FOR
BEEF COWS AND PROFITS FOR A
REPRESENTATIVE FARM IN THE
GEORGIA PIEDMONT
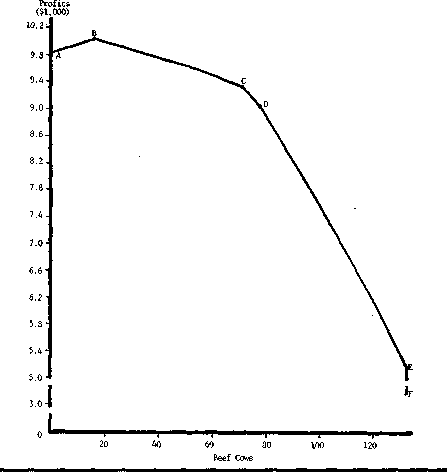
Table 2. SELECTED POINTS ON THE BEEF
COW-PROFIT FRONTIER FOR A
REPRESENTATIVE FARM IN THE
GEORGIA PIEDMONT
|
Profits |
Beef Cows |
Rate of |
|
9,848 |
0 |
-12.85 |
|
10,004 |
12 |
-11.04 |
|
10,036 |
15 |
- 5.31 |
|
10,041 |
16 |
2.49 |
|
10,039 |
17 |
11.22 |
|
9,927 |
27 |
11.76 |
|
9,722 |
44 |
12.27 |
|
9,620 |
53 |
14.34 |
|
9,415 |
67 |
16.47 |
|
9,403 |
68 |
18.84 |
|
9,380 |
69 |
20.59 |
|
9,332 |
71 |
37¾13 |
|
9,267 |
73 |
44.12 |
|
9,171 |
75 |
45.42 |
|
9,062 |
77 |
51.90 |
|
9,056 |
78 |
62.49 |
|
8,493 |
87 |
66.39 |
|
7,811 |
97 |
68.67 |
|
6,799 |
112 |
72.06 |
|
6,181 |
120 |
73.52 |
|
6,035 |
122 |
76.35 |
|
5,868 |
124 |
77.71 |
|
5,173 |
133 | |
|
3,195 |
133 |
farm allow production of a maximum of 133
cows which are associated with a profit level of
$5,173 at point E. Complete specialization in 133
beef cows yield profits of $3,195 (point F).
Within the range of consicuous production,
92