mode of the distribution of the ex post rates conveys some rough indication of the implicit
cutoff rate used in the ex ante optimal selection procedure.
In order to distill information on the slope of the ex ante distribution from a sample of ex post
rates of return some strict assumptions have to be made. Figure 3 sketches the problem that needs to
be tackled. Due to suboptimal selection, some of the projects with an ERR higher than the cutoff rate
are not selected, while projects with an ERR lower than the cutoff rate are. It is assumed that all
projects cost the same. If the selection were optimal, only R&D projects at or above the cutoff rate
would have been selected. In order to reconstruct the ex ante optimal distribution, the right-hand side
of the distribution has to be topped up with the number of R&D projects below the cutoff rate.
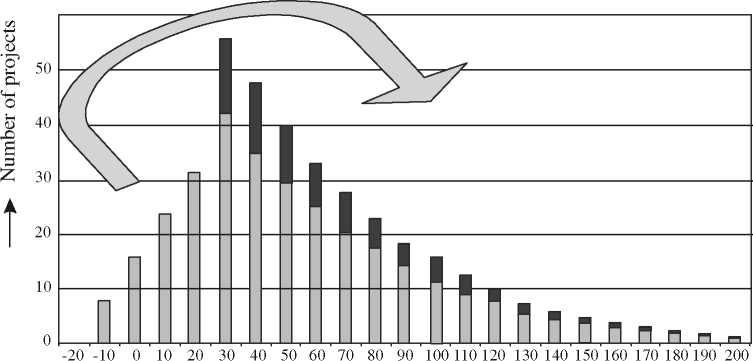
Expected rate of return (ERR)
□ Suboptimal selection □ Reallocation of projects from below the cutoff rate
Figure 3: Reconstruction of the optimal selection of R&D projects
Of the various options available, distributing the suboptimal R&D projects proportionally
seems to give a reasonable approximation and has the practical advantage that the adjusted and
unadjusted right-hand side of the distribution has the same slope coefficient. However, a proportional
distribution implies that the chance of not being selected is the same for all R&D projects above the
cutoff rate. A more realistic assumption is that R&D projects close to the cutoff rate have a higher
chance of not being selected than projects with higher ERRs. Such a differential in chance would lead
More intriguing information
1. The name is absent2. The name is absent
3. The name is absent
4. Iconic memory or icon?
5. The name is absent
6. The name is absent
7. The name is absent
8. Implementation of Rule Based Algorithm for Sandhi-Vicheda Of Compound Hindi Words
9. Washington Irving and the Knickerbocker Group
10. The name is absent