Stata Technical Bulletin
Bishop, Y. M. M., S. E. Fienberg, and P. W. Holland. 1975. Discrete Multivariate Analysis. Cambridge, MA: MIT Press.
Gilbert, N. 1993. Analyzing tabular data: loglinear and logistic models for social researchers. London: UCL Press.
Haberman, S. J. 1973. The analysis of residuals in cross-classified tables. Biometrics 29: 205-220.
Judson, D. H. 1992a. smv5: Performing loglinear analysis of cross-classifications. Stata Technical Bulletin 6: 7-17.
——. 1992b. smv5.1: Loglinear analysis of cross-classifications, update. Stata Technical Bulletin 8: 18.
Tivers, J. 1985. Women Attached: The Daily Lives of Women with Young Children. Beckenham, UK: Croom Helm.
sg58 Mountain plots
Richard Goldstein, Qualitas, Inc., [email protected]
There are numerous options, both in Stata and in the literature, for graphically displaying univariate distributions. Examples
in Stata include box plots, probability plots, histograms, stem-and-leaf plots, etc. One family of such plots display the empirical
distribution function (EDF). The mountain plot presented here is a member of this family.
In effect, a mountain plot is a folded EDF curve (Monti 1995). A mountain plot for the price variable from Stata’s
auto.dta dataset is shown in Figure 1.
. mountain price
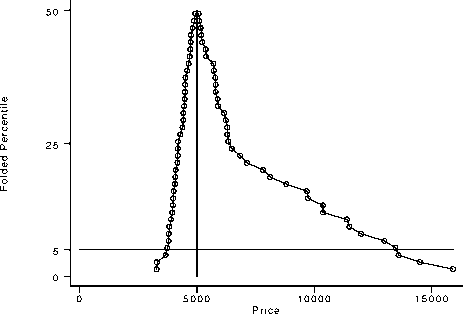
Monti's Mountain Plot
Figure 1
Monti points out that by examining such a plot it is easy to perform the following:
1. Determine the median.
2. Determine the range.
3. Determine the central or tail percentiles of any magnitude.
4. Observe outliers.
5. Observe unusual gaps in the data.
6. Examine the data for symmetry.
7. Compare several distributions.
8. Visually gauge the sample size (if plotting symbols are used).
(Note: the implementation here requires a little work on the part of the user to perform number 7 in the above list.)
Given the relationship between the mountain plot and the EDF plot, it is clear that they provide the same information;
however, some of the information is much easier to see in the mountain plot, including the median (and other percentiles), and
assessing symmetry. On the other hand, as Monti points out, there are limitations to the mountain plot (e.g., the density curve
is obscured).
The syntax of mountain is
mountain varname [if exp [in range [, nograph graph_options ]
More intriguing information
1. Special and Differential Treatment in the WTO Agricultural Negotiations2. Education Research Gender, Education and Development - A Partially Annotated and Selective Bibliography
3. The fundamental determinants of financial integration in the European Union
4. The name is absent
5. The name is absent
6. Short Term Memory May Be the Depletion of the Readily Releasable Pool of Presynaptic Neurotransmitter Vesicles
7. Income Growth and Mobility of Rural Households in Kenya: Role of Education and Historical Patterns in Poverty Reduction
8. Integrating the Structural Auction Approach and Traditional Measures of Market Power
9. Improvements in medical care and technology and reductions in traffic-related fatalities in Great Britain
10. Altruism with Social Roots: An Emerging Literature